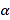题目内容
【题目】有一块半径为![]() ,圆心角为
,圆心角为![]() 的扇形钢板,需要将它截成一块矩形钢板,分别按图1和图2两种方案截取(其中方案二中的矩形关于扇形的对称轴对称).
的扇形钢板,需要将它截成一块矩形钢板,分别按图1和图2两种方案截取(其中方案二中的矩形关于扇形的对称轴对称).
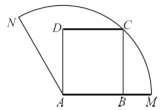
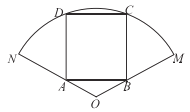
图1:方案一 图2:方案二
(1)求按照方案一截得的矩形钢板面积的最大值;
(2)若方案二中截得的矩形![]() 为正方形,求此正方形的面积;
为正方形,求此正方形的面积;
(3)若要使截得的钢板面积尽可能大,应选择方案一还是方案二?请说明理由,并求矩形钢板面积的最大值.
【答案】(1)25(2)![]() (3)方案二,最大值为
(3)方案二,最大值为![]() ,理由见解析
,理由见解析
【解析】
(1)连接![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,则矩形面积为关于
,则矩形面积为关于![]() 的函数,求出最值即可;
的函数,求出最值即可;
(2)连接![]() ,设
,设![]() ,利用正弦定理和三角形的对称性质可得
,利用正弦定理和三角形的对称性质可得![]()
![]() ,利用
,利用![]() 解得
解得![]() ,进而求出正方形面积即可;
,进而求出正方形面积即可;
(3)由(2)得到![]() ,求出最大值,与(1)的最值比较即可
,求出最大值,与(1)的最值比较即可
解:(1)连接![]() ,设
,设![]() ,
,![]() ,
,
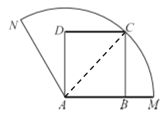
则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() ,即
,即![]() 时,
时,![]()
(2)连接![]() ,设
,设![]()
![]() ,
,
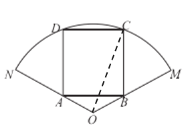
![]() 正方形关于扇形轴对称,
正方形关于扇形轴对称,
![]()
![]()
![]() ,
,
则![]() ,
,
在![]() 中,由正弦定理可得
中,由正弦定理可得![]() ,即
,即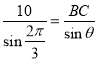 ,
,
则![]() ,
,
![]() 正方形,
正方形,
![]() ,即
,即![]() ,则
,则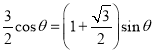 ,
,
代入![]() 可得
可得![]() ,
,
则![]()
(3)选择方案二,
由(2),对于方案二
![]()
![]() ,
,
![]() 当
当![]() ,即
,即![]() 时,
时,![]()
由(1)![]() ,
,
应选择方案二

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】某商家对他所经销的一种商品的日销售量(单位:吨)进行统计,最近50天的统计结果
如下表:
日销售量 | 1 | 1.5 | 2 |
天数 | 10 | 25 | 15 |
频率 | 0.2 |
|
|
若以上表中频率作为概率,且每天的销售量相互独立.
(1)求5天中该种商品恰好有两天的销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元,表示该种商品某两天销售利润的和(单位:千元),求的分布列和数学期望.