题目内容
【题目】已知五边形ABECD由一个直角梯形ABCD与一个等边三角形BCE构成,如图1所示,AB丄BC,AB//CD,且AB=2CD。将梯形ABCD沿着BC折起,如图2所示,且AB丄平面BEC。
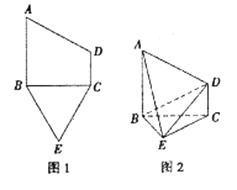
(1)求证:平面ABE丄平面ADE;
(2)若AB=BC,求二面角A-DE-B的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() 的中点
的中点![]() ,连接
,连接![]() ,可证得四边形
,可证得四边形![]() 为平行四边形,可得
为平行四边形,可得![]() .由条件可得到
.由条件可得到![]() 平面
平面![]() ,从而
,从而![]() 平面
平面![]() ,于是可得所证结论成立.(2)建立空间直角坐标系,再求出两个平面的法向量,根据两法向量的夹角可求出二面角的平面角的余弦值.
,于是可得所证结论成立.(2)建立空间直角坐标系,再求出两个平面的法向量,根据两法向量的夹角可求出二面角的平面角的余弦值.
(1)证明:取![]() 的中点
的中点![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
则![]() 且
且![]() .
.
∵![]() 且
且![]() ,
,
∴![]() 且
且![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() .
.
∵img src="http://thumb.zyjl.cn/questionBank/Upload/2019/07/10/08/7c111f09/SYS201907100800588825886904_DA/SYS201907100800588825886904_DA.020.png" width="163" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
∴![]() 平面
平面![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)过![]() 作
作![]() 于
于![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() 平面
平面![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴,过
轴,过![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
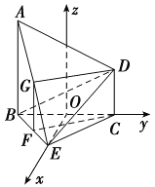
设![]() ,则
,则![]()
∴![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则有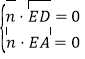 ,即
,即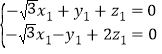 ,
,
取![]() 得
得![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则有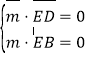 ,即
,即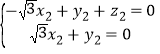 ,
,
取![]() ,得
,得![]() ,则
,则![]() .
.
∴![]() ,
,
又由图可知二面角![]() 的平面角为锐角,
的平面角为锐角,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.