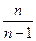题目内容

已知曲线y=
1
2
x2-2上一点P（1，-
3
2
），则过点P的切线的倾斜角为（　　）
A．30°B．45°C．135°D．150°
函数y=
1
2
x2-2的导数为f′（x）=x，则函数在点P处的切线斜率为k=f′（1）=1．
设切线的倾斜角为θ，则tanθ=1，所以θ=45°．
即过点P的切线的倾斜角为45°．
故选B．
练习册系列答案
相关题目
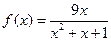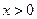（本小题满分12分）已知函数 () , (Ⅰ)试确定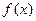的单调区间 , 并证明你的结论 ;(Ⅱ)若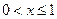时 , 不等式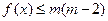恒成立 , 求实数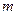的取值范围 .
设函数f（x）=cos（
3
x+φ）（-π＜φ＜0）．若f（x）+f′（x）是偶函数，则φ=（　　）
A．
π
3
B．-
π
3
C．
π
6
D．-
π
6
已知函数f(x)=
1
3
x3-ax2+(a2-1)x(a∈R，a≠0)的导数f′（x）的图象如图所示，则f（1）=（　　）
A．
4
3
B．-
2
3
C．-
2
3
或
4
3
D．以上都不正确
设函数f（x）=
1
2
（sinx-cosx）的导函数为f′（x），则下列结论正确的是（　　）
A．f′（x）+f（x）=-sinxB．f′（x）+f（x）=-cosx
C．f′（x）-f（x）=sinxD．f′（x）-f（x）=cosx
设函数的导函数，则数列的前n项和是
（   ）
A．B．C．D．
函数y=lnx+1的导数是（　　）
A．
1
x
B．
1
x+1
C．lnxD．ex
已知f（x）=lnx，则f′(
π
2
)=（　　）
A．ln(
π
2
)		B．
2
π
C．
π
2
D．-1
已知f(x)=
π
2
+cosx，则f′（
π
2
）=（　　）
A．-1+
π
2
B．-1C．1D．0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网