题目内容
四棱锥 的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形,
的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形, ,
,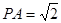 ,则该球的体积为 _
,则该球的体积为 _
 的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形,
的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形, ,
,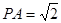 ,则该球的体积为 _
,则该球的体积为 _ 
试题分析:四棱锥P-ABCD,扩展为长方体,长方体的对角线的长就是外接球的直径,
所以R=
 ,所以球的体积为:
,所以球的体积为: .
.
练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
题目内容
 的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形,
的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形, ,
,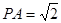 ,则该球的体积为 _
,则该球的体积为 _ 
 ,所以球的体积为:
,所以球的体积为: .
.
 互动英语系列答案
互动英语系列答案