题目内容
如图,△ 中,
中, ,
, ,
,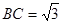 ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心 在边
在边 上,半圆与
上,半圆与 、
、 分别相切于点
分别相切于点 、
、 ,与
,与 交于点
交于点 ),将△
),将△ 绕直线
绕直线 旋转一周得到一个旋转体.
旋转一周得到一个旋转体.

(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线 旋转一周所得旋转体的体积.
旋转一周所得旋转体的体积.
 中,
中, ,
, ,
,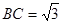 ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心 在边
在边 上,半圆与
上,半圆与 、
、 分别相切于点
分别相切于点 、
、 ,与
,与 交于点
交于点 ),将△
),将△ 绕直线
绕直线 旋转一周得到一个旋转体.
旋转一周得到一个旋转体.
(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线
 旋转一周所得旋转体的体积.
旋转一周所得旋转体的体积.(1)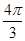 ;(2)
;(2)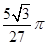 .
.
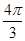 ;(2)
;(2)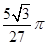 .
.试题分析:(1)要求球的表面积,首先要求出球的半径,如图即半圆
 的半径,这可在
的半径,这可在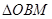 中列方程解得,圆
中列方程解得,圆 半径为
半径为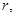 则有
则有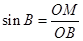 ,即
,即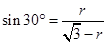 ,则此求得
,则此求得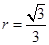 ;(3)要阴影部分旋转后的体积,我们要看阴影部分是什么几何体,看看能不能把变成我们熟知的锥台、球,或者上它们构成的,本题中,是在三角形内部挖去一个小三角形,因此最后所得可以看作是一个圆锥里面挖去了一个球,从而其体积就等于一个圆锥的体积减去球的体积,即
;(3)要阴影部分旋转后的体积,我们要看阴影部分是什么几何体,看看能不能把变成我们熟知的锥台、球,或者上它们构成的,本题中,是在三角形内部挖去一个小三角形,因此最后所得可以看作是一个圆锥里面挖去了一个球,从而其体积就等于一个圆锥的体积减去球的体积,即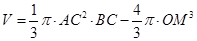 .
.试题解析:(1)连接
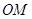 ,则
,则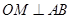 ,
,设
 ,则
,则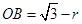 ,
,在
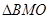 中,
中,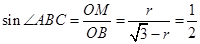 ,
,所以
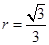 (4分)
(4分)所以
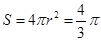 . (6分)
. (6分)(2)
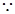
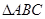 中,
中,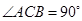 ,
,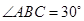 ,
,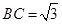 ,
,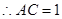 , (8分)
, (8分)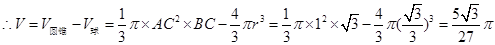 .(12分)
.(12分)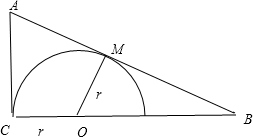

练习册系列答案
相关题目
 是母线
是母线 的中点,
的中点, 是底面圆的直径,半径
是底面圆的直径,半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于 .
.
 与
与 所成的角;
所成的角; 中,
中,
 底面
底面 ,
, ,
, ,
, .
.
 平面
平面 ;
; ,求四棱锥
,求四棱锥 的体积.
的体积. 平面
平面 ,且四边形
,且四边形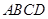 为矩形,四边形
为矩形,四边形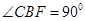 ,
,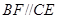 ,
,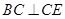 ,
,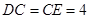 ,
,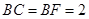 .
.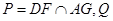 是直线
是直线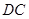 上的动点,判断并证明直线
上的动点,判断并证明直线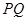 与直线
与直线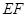 的位置关系.
的位置关系.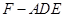 的体积..
的体积..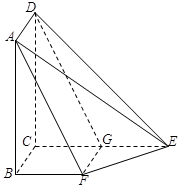
 中,
中, 则四面体外接球的表面积为( )
则四面体外接球的表面积为( )
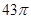





 的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形,
的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形, ,
,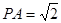 ,则该球的体积为 _
,则该球的体积为 _ 