题目内容
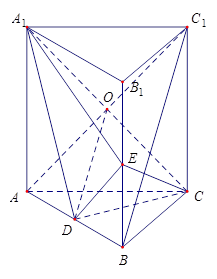
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.
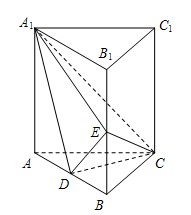
(1)证明:BC1//平面A1CD;
(2)设AA1=AC=CB=2,AB=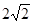 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.

(1)证明:BC1//平面A1CD;
(2)设AA1=AC=CB=2,AB=
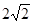 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.(1)详见解析;(2)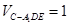 .
.
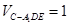 .
.试题分析:(1)根据线面平行的判定定理,需在平面
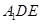 内找一条与
内找一条与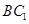 平行的直线.因为
平行的直线.因为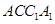 是矩形,故对角线互相平分,所以连结
是矩形,故对角线互相平分,所以连结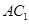 ,与
,与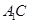 交于点O;因为D是AB的中点,连结
交于点O;因为D是AB的中点,连结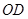 ,则
,则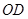 是
是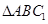 的中位线,所以
的中位线,所以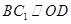 ,从而可证得
,从而可证得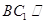 平面
平面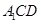 .(2)易得
.(2)易得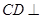 平面
平面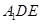 .所以
.所以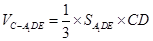 .因为
.因为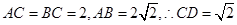 .求
.求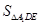 可用矩形的面积减去周围三个三角形的面积.从而求得三棱锥
可用矩形的面积减去周围三个三角形的面积.从而求得三棱锥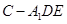 的体积..
的体积..试题解析:(1)连结
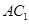 ,与
,与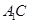 交于点O,连结
交于点O,连结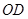 ,因为D是AB的中点,所以
,因为D是AB的中点,所以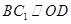 ,因为
,因为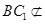 平面
平面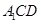 ,
,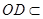 平面
平面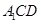 ,所以
,所以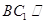 平面
平面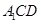 .
.(2)因为
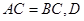 为
为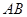 的中点,所以
的中点,所以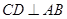 ,又因为该三棱柱是直三棱柱,所以
,又因为该三棱柱是直三棱柱,所以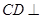 平面
平面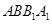 ,即
,即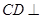 平面
平面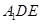 .所以
.所以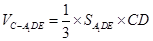 .因为
.因为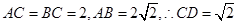 .
.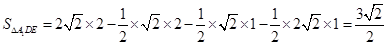 .所以
.所以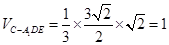 .
.

练习册系列答案
相关题目
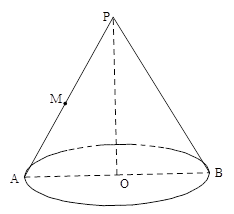
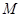 是母线
是母线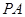 的中点,
的中点,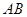 是底面圆的直径,半径
是底面圆的直径,半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于 .
.
 与
与 所成的角;
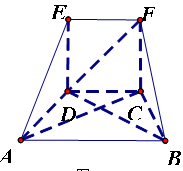
所成的角;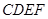 为正方形,四边形
为正方形,四边形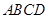 为等腰梯形,
为等腰梯形, ,
,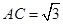 ,
,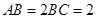 ,
,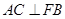 .
.
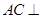 平面
平面 ;
;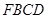 的体积;
的体积; 上是否存在点
上是否存在点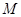 ,使
,使 平面
平面 ?请证明你的结论.
?请证明你的结论.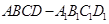 中,
中,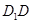
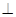 底面
底面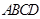 ,
, ,
, ,
,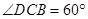 .
.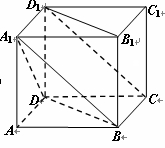
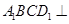 平面
平面 ;
;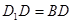 ,求四棱锥
,求四棱锥 的体积.
的体积. ,E为侧棱PC的中点,则PA与BE所成的角为__________.
,E为侧棱PC的中点,则PA与BE所成的角为__________.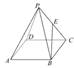
 中,
中,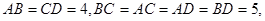 则四面体外接球的表面积为( )
则四面体外接球的表面积为( )



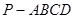 的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形,
的五个顶点都在一个球面上,且底面ABCD是边长为1的正方形,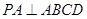 ,
,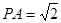 ,则该球的体积为 _
,则该球的体积为 _ 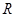 的圆柱形量杯中装有适量的水若放入一个半径为
的圆柱形量杯中装有适量的水若放入一个半径为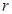 的实心铁球,水面高度恰好升高
的实心铁球,水面高度恰好升高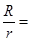 ____________.
____________.