题目内容
4.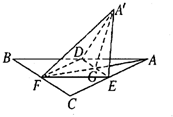 如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 异面直线A′E与BD不可能垂直 | |
| B. | 恒有平面A′GF⊥平面BCDE | |
| C. | 三棱锥A′-EFD的体积有最大值 | |
| D. | 动点A′在平面ABC上的射影在线段AF上 |
分析 A.建立空间直角坐标系,不妨设BC=4,则E(0,1,0),B$(\sqrt{3},-2,0)$,A$(-\sqrt{3},0,0)$,A′(x,0,z).由$\overrightarrow{{A}^{′}E}•\overrightarrow{AB}$=$-2\sqrt{3}x-2$=0,解得x,因此取A′$(-\frac{\sqrt{3}}{3},0,\frac{\sqrt{26}}{3})$,可得A′E⊥AB,即可判断出正误;
B.由于ED⊥FG,ED⊥GA′,可得ED⊥平面A′GF,即可判断出正误;
C.恒有平面A′DE⊥平面BCDE时,三棱锥A′-EFD的体积有最大值$\frac{1}{3}{S}_{△DEF}•{A}^{′}G$,即可判断出正误;
D.由A可知动点:A′在平面ABC上的射影在线段AF上,即可判断出正误.
解答 解:如图所示,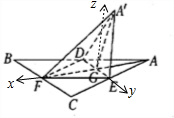
A.建立空间直角坐标系,不妨设BC=4,则E(0,1,0),B$(\sqrt{3},-2,0)$,A$(-\sqrt{3},0,0)$,A′(x,0,z).$\overrightarrow{{A}^{′}E}$=(-x,1,-z),$\overrightarrow{AB}$=$(2\sqrt{3},-2,0)$,由$\overrightarrow{{A}^{′}E}•\overrightarrow{AB}$=$-2\sqrt{3}x-2$=0,解得x=$-\frac{\sqrt{3}}{3}$,z=$\sqrt{(\sqrt{3})^{2}-(\frac{\sqrt{3}}{3})^{2}}$=$\frac{\sqrt{26}}{3}$.因此取A′$(-\frac{\sqrt{3}}{3},0,\frac{\sqrt{26}}{3})$,可得A′E⊥AB,因此A不正确.
B.∵ED⊥FG,ED⊥GA′,FG∩GA′,∴ED⊥平面A′GF,∴恒有平面A′GF⊥平面BCDE.
C.恒有平面A′DE⊥平面BCDE时,三棱锥A′-EFD的体积有最大值$\frac{1}{3}{S}_{△DEF}•{A}^{′}G$,正确;
D.由A可知动点:A′在平面ABC上的射影在线段AF上,正确.
故选:A.
点评 本题考查了线面面面垂直的判定与性质定理、勾股定理、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

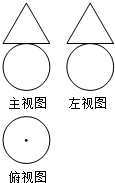 某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的表面积为( )| A. | $\frac{4+\sqrt{3}}{3}$π | B. | 5π | C. | 6π | D. | 7π |
| A. | (-∞,4-8ln2] | B. | (-∞,$\frac{17}{4}$-8ln2] | C. | (-∞,4+8ln2] | D. | (-∞,$\frac{17}{4}$+8ln2] |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | π |
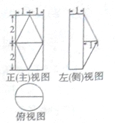
| A. | $\frac{16}{3}$ | B. | 5+$\frac{π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |