题目内容

19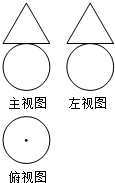．某几何体的三视图如图所示，其中三角形的三边长与圆的直径均为2，则该几何体的表面积为（　　）
A．$\frac{4+\sqrt{3}}{3}$πB．5πC．6πD．7π

分析 根据几何体的三视图，得出该几何体是球与圆锥的组合体，结合图中数据求出它的表面积．

解答 解：根据几何体的三视图，得：
该几何体是底部为球体，上部为圆锥体的组合体，
且球的半径与圆锥底面圆的半径都为1，
圆锥的母线长为2；
所以，球的表面积为4π•12=4π，
圆锥体的表面积为π•12+π•1•2=3π，
该几何体的表面积为4π+3π=7π．
故选：D．

点评 本题考查了利用空间几何体的三视图求表面积的应用问题，解题的关键是由三视图得出几何体的结构特征．

练习册系列答案
相关题目
9．已知f（n）=1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$，g（n）=$\frac{1}{2}$（3-$\frac{1}{{n}^{2}}$），n∈N*．
（1）当n=1，2，3时，试比较f（n）与g（n）的大小关系；
（2）猜想f（n）与g（n）的大小关系，并用数学归纳法证明．
10．下列类比推理中，结论正确的个数是（　　）
①由a（b+c）=ab+ac类比得到loga（x+y）=logax+logay
②由a（b+c）=ab+ac类比得到sin（x+y）=sinx+siny
③由（ab）n=anbn类比得到（x+y）n=xn+yn
④由（a+b）+c=a+（b+c）类比得到（xy）z=x（yz）
A．0B．1C．2D．3
7．由抛物线y2=$\frac{x}{5}$，y2=x-1所围成封闭图形的面积为$\frac{2}{3}$．
14．若二项式（x2-$\frac{2}{x}$）n展开式的第5项是常数项，则展开式的中间项为（　　）
A．-160B．-160x3C．20D．160x3
4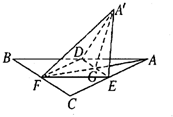．如图，等边三角形ABC的中线AF与中位线DE相交于G，已知△A′ED是△ADE绕DE旋转过程中的一个图形，下列命题中，错误的是（　　）
A．异面直线A′E与BD不可能垂直
B．恒有平面A′GF⊥平面BCDE
C．三棱锥A′-EFD的体积有最大值
D．动点A′在平面ABC上的射影在线段AF上
11．已知向量$\overrightarrow{a}$=（cos$\frac{3}{2}$x，sin$\frac{3}{2}$x），$\overrightarrow{b}$=（cos$\frac{x}{2}$，sin$\frac{x}{2}$），且x∈[0，$\frac{2π}{3}$]．
（1）求$\overrightarrow{a}$•$\overrightarrow{b}$及|$\overrightarrow{a}$+$\overrightarrow{b}$|；
（2）若f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$-2λ|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值为-$\frac{3}{2}$，求实数λ的值．
8．（1）已知数列{an}的前n项和为Sn，若${S_n}={3^n}+2n+1$，求an
（2）等差数列{an}的前n项和记为Sn，已知a10=30，a20=50，Sn=242，求n．
9．若函数f（x）=sin2ax-$\sqrt{3}$sinax•cosax-$\frac{1}{2}$（a＞0）的图象与直线y=b相切，并且切点的横坐标依次成公差为$\frac{π}{2}$的等差数列．
（Ⅰ）求a，b的值；
（Ⅱ）若x0∈[0，$\frac{π}{2}$]，且x0是y=f（x）的零点，试写出函数y=f（x）在[x0，x0+$\frac{π}{2}$]上的单调增区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网