题目内容
16.若f(x)=sin(2x+φ)为偶函数,则φ值可能是( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | π |
分析 由条件根据正弦函数、余弦函数的奇偶性以及诱导公式,可得φ=kπ+$\frac{π}{2}$,k∈z,从而得出结论.
解答 解:若f(x)=sin(2x+φ)为偶函数,则φ=kπ+$\frac{π}{2}$,k∈z,∴φ的值可能是$\frac{π}{2}$,
故选:B.
点评 本题主要考查正弦函数、余弦函数的奇偶性以及诱导公式,属于基础题.

练习册系列答案
相关题目
6.sin600°=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
4.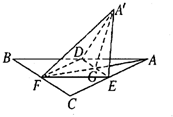 如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
 如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边三角形ABC的中线AF与中位线DE相交于G,已知△A′ED是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 异面直线A′E与BD不可能垂直 | |
| B. | 恒有平面A′GF⊥平面BCDE | |
| C. | 三棱锥A′-EFD的体积有最大值 | |
| D. | 动点A′在平面ABC上的射影在线段AF上 |
6.若函数f(x)=log${\;}_{\frac{1}{2}}$(-x2+4x+5)在区间(3m-2,m+2)内单调递增,则实数m的取值为( )
| A. | [$\frac{4}{3},3$] | B. | [$\frac{4}{3},2$] | C. | [$\frac{4}{3},2$) | D. | [$\frac{4}{3},+∞$) |