题目内容
设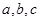 为三角形
为三角形 的三边,求证:
的三边,求证:
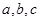 为三角形
为三角形 的三边,求证:
的三边,求证:
见解析
试题分析:利用分析法证明,可先将分式不等式转化为整式不等式,然后利用三角形两边之和大于第三边即可.
证明:要证明:

需证明:a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b) 4分
需证明:a(1+b+c+bc)+ b(1+a+c+ac)> c(1+a+b+ab) 需证明a+2ab+b+abc>c 8分
∵a,b,c是
 的三边 ∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0
的三边 ∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0 ∴a+2ab+b+abc>c
∴
 成立。 12分
成立。 12分
练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 ,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1.
,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1. 是一个自然数,
是一个自然数, 是
是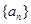 :
: 是自然数,
是自然数, (
( ,
, ).
). ,
, ;
; ,求证:
,求证: ;
; 时,求证:存在
时,求证:存在 ,使得
,使得 .
.
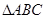 中,
中,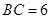 ,以
,以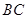 为直径的半圆分别交
为直径的半圆分别交 于点
于点 ,若
,若 ,则
,则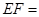


 ,且
,且 求证:
求证: 中至少有一个是负数。
中至少有一个是负数。