题目内容
在Rt△OAB中,∠O=90°,则cos2A+cos2B=1.根据类比推理的方法,在三棱锥O-ABC中,OA⊥OB,OB⊥OC,OC⊥OA,α、β、γ分别是三个侧面与底面所成的二面角,则______.
在Rt△OAB中,cos2A+cos2B=(
)2+(
)2=
=1.
∵OA⊥OB,OB⊥OC,OC⊥OA,∴三个侧面两两互相垂直,
于是类比到三棱锥O-ABC中,猜想三棱锥O-ABC中,若三个侧面分别与底面所成的角为α、β、γ,则cos2α+cos2β+cos2γ=1.故答案为cos2α+cos2β+cos2γ=1.
| b |
| c |
| a |
| c |
| a2+b2 |
| c2 |
∵OA⊥OB,OB⊥OC,OC⊥OA,∴三个侧面两两互相垂直,
于是类比到三棱锥O-ABC中,猜想三棱锥O-ABC中,若三个侧面分别与底面所成的角为α、β、γ,则cos2α+cos2β+cos2γ=1.故答案为cos2α+cos2β+cos2γ=1.

练习册系列答案
相关题目
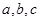 为三角形
为三角形 的三边,求证:
的三边,求证:

 ,请你写出一个具有一般性的等式,使你写出的等式包含了已知的等式(不要求证明),这个等式是_________ .
,请你写出一个具有一般性的等式,使你写出的等式包含了已知的等式(不要求证明),这个等式是_________ .
 ,使得
,使得 能被
能被 三数成等比数列,而
三数成等比数列,而 分别为
分别为 和
和 的等差中项,则
的等差中项,则 ( )
( )

