题目内容
15.函数f(x)=$\frac{cosx}{ln(|x|+1)}$图象大致是( )| A. | 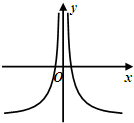 | B. | 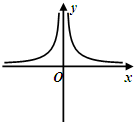 | C. |  | D. | 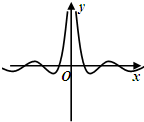 |
分析 由已知中函数f(x)=$\frac{cosx}{ln(|x|+1)}$的解析式,分析出函数的定义域,奇偶性,及当x>0时,函数零点的个数及图象的位置,利用排除法可得答案.
解答 解:∵f(x)的定义域是{x|x≠0},且是偶函数,可排除C;
当x>0时,分母为恒为正值,分子符号不定,即x>0时,f(x)不可能恒为正值,可排除B;
当x>0时,f(x)不可能只有一个零点,可排除A.
(当x→+∞时,分子|cosx|≤1,分母ln(|x|+1)→+∞,∴f(x)→0,排除A.)
故选:D.
点评 本题考查的知识点是函数的图象,是函数图象和性质的综合应用,本题直接画图难度较大,多采用排除法解答.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
3.已知a>0,b>0,a+b=1则-$\frac{1}{2a}-\frac{2}{b}$的最大值为( )
| A. | -3 | B. | -4 | C. | $-\frac{1}{4}$ | D. | $-\frac{9}{2}$ |
10.已知f(x)为R上的可导函数,且对?x∈R,f(x)>f′(x),则有( )
| A. | e2015f(-2015)<f(0),f(2015)>e2015f(0) | B. | e2015f(-2015)<f(0),f(2015)<e2015f(0) | ||
| C. | e2015f(-2015)>f(0),f(2015)>e2015f(0) | D. | e2015f(-2015)>f(0),f(2015)<e2015f(0) |
5.在△ABC中,a=$\sqrt{3}$,b=1,A=60°,则B等于( )
| A. | 30° | B. | 60° | C. | 150° | D. | 45° |