题目内容
20.用一个平面去截球所得的截面面积为2πcm2,已知球心到该截面的距离为1cm,则该球的体积为4√3√3πcm3.分析 求出小圆的半径,然后利用球心到该截面的距离为1cm,小圆的半径,通过勾股定理求出球的半径,即可求出球的体积.
解答 解:用一平面去截球所得截面的面积为2π cm2,所以小圆的半径为:√2√2cm;
已知球心到该截面的距离为1cm,所以球的半径为:√1+2√1+2=
所以球的体积为:43π•(√3)3=4√3π(cm3)
故答案为:4√3π.
点评 本题是基础题,考查球的小圆的半径,球心到该截面的距离,球的半径之间的关系,满足勾股定理,考查计算能力.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
15.函数f(x)=cosxln(|x|+1)图象大致是( )
| A. | 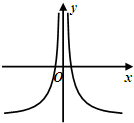 | B. | 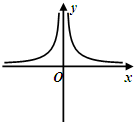 | C. |  | D. | 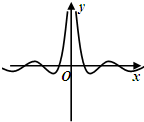 |
5.以下选项中正确的是( )
| A. | a=7,b=14,A=30°△ABC有两解 | B. | a=9,c=10,A=60°△ABC无解 | ||
| C. | a=6,b=9,A=45°△ABC有两解 | D. | a=30,b=25,A=150°△ABC有一解 |
 将棱长相等的正方体按右图所示的形状摆放,从上往下依次为第1层,第2层,第3层,…,则第n层正方体的个数是
将棱长相等的正方体按右图所示的形状摆放,从上往下依次为第1层,第2层,第3层,…,则第n层正方体的个数是