题目内容
已知集合M是满足下列性质函数的f(x)的全体,在定义域D内存在x0,使得f(x0+1)=f(x0)+f(1)成立.
(1)函数f(x)=
,g(x)=x2是否属于集合M?分别说明理由.
(2)若函数f(x)=lg
属于集合M,求实数a的取值范围.
(1)函数f(x)=
| 1 |
| x |
(2)若函数f(x)=lg
| a |
| x2+1 |
(1)对于函数f(x)=
,D=(-∞,0)∪(0,+∞),若f(x)∈M,
则存在非零实数x0,使得
=
+1,即x02+x0+1=0,显然此方程无实数解,
∴f(x)∉M;
函数g(x)=x2,D=R,若g(x)∈M成立,
则有(x0+1)2=x02+1,解得x0=0,
∴g(x)∈M;
(2)由条件得:D=R,a>0,由f(x)∈M知,
存在实数x0,使得lg
=lg
+lg
,
∴
=
•
,
化简得:(a-2)x02+2ax0+2a-2=0,
当a=2时,x0=-
,符号题意;
当a≠2时,由△≥0得:4a2-4(a-2)(2a-2)≥0,
即3-
≤a≤3+
(a≠2),
综上所述,a的取值范围是[3-
,3+
].
| 1 |
| x |
则存在非零实数x0,使得
| 1 |
| x0+1 |
| 1 |
| x0 |
∴f(x)∉M;
函数g(x)=x2,D=R,若g(x)∈M成立,
则有(x0+1)2=x02+1,解得x0=0,
∴g(x)∈M;
(2)由条件得:D=R,a>0,由f(x)∈M知,
存在实数x0,使得lg
| a |
| (x0+1)2+1 |
| a |
| x02+1 |
| a |
| 2 |
∴
| a |
| (x0+1)2+1 |
| a |
| x02+1 |
| a |
| 2 |
化简得:(a-2)x02+2ax0+2a-2=0,
当a=2时,x0=-
| 1 |
| 2 |
当a≠2时,由△≥0得:4a2-4(a-2)(2a-2)≥0,
即3-
| 5 |
| 5 |
综上所述,a的取值范围是[3-
| 5 |
| 5 |

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
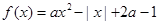 (
(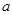 为实常数).
为实常数).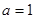 ,求函数
,求函数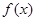 的单调区间;
的单调区间;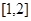 上的最小值为
上的最小值为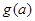 ,求
,求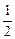 )
)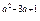 的单调递减区间.
的单调递减区间.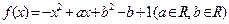 ,对任意实数
,对任意实数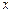 都有
都有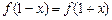 成立,若当
成立,若当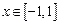 时,
时,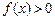 恒成立,则
恒成立,则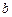 的取值范围是 ▲ .
的取值范围是 ▲ . ,则
,则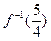 =
=