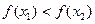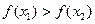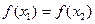题目内容
已知奇函数f(x)对任意x,y∈R,总有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(1)=-
.
(1)求证:f(x)是R上的减函数.
(2)求f(x)在[-3,3]上的最大值和最小值.
(3)若f(x)+f(x-3)≤-2,求实数x的取值范围.
| 2 |
| 3 |
(1)求证:f(x)是R上的减函数.
(2)求f(x)在[-3,3]上的最大值和最小值.
(3)若f(x)+f(x-3)≤-2,求实数x的取值范围.
(1)证明:令x=y=0,则f(0)=0,令y=-x则f(-x)=-f(x),---2’
在R上任意取x1,x2,且x1<x2,则△x=x2-x1>0,△y=f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1)------4分
∵x2>x1,
∴x2-x1>0,
又∵x>0时,f(x)<0,
∴f(x2-x1)<0,即f(x2)-f(x1)<0,有定义可知函数f(x)在R上为单调递减函数.--6分
(2)∵f(x)在R上是减函数,
∴f(x)在[-3,3]上也是减函数.
又f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=3×(-
)=-2,
由f(-x)=-f(x)可得f(-3)=-f(3)=2,
故f(x)在[-3,3]上最大值为2,最小值为-2.------10分
(3)∵f(x)+f(x-3)≤-2,由(1)、(2)可得f(2x-3)≤f(3)
∴2x-3≥3,
∴x≥3,
故实数x的取值范围为[3,+∞).------12分
在R上任意取x1,x2,且x1<x2,则△x=x2-x1>0,△y=f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1)------4分
∵x2>x1,
∴x2-x1>0,
又∵x>0时,f(x)<0,
∴f(x2-x1)<0,即f(x2)-f(x1)<0,有定义可知函数f(x)在R上为单调递减函数.--6分
(2)∵f(x)在R上是减函数,
∴f(x)在[-3,3]上也是减函数.
又f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=3×(-
| 2 |
| 3 |
由f(-x)=-f(x)可得f(-3)=-f(3)=2,
故f(x)在[-3,3]上最大值为2,最小值为-2.------10分
(3)∵f(x)+f(x-3)≤-2,由(1)、(2)可得f(2x-3)≤f(3)
∴2x-3≥3,
∴x≥3,
故实数x的取值范围为[3,+∞).------12分

练习册系列答案
相关题目
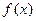 的定义域为
的定义域为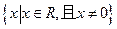 对定义域内的任意
对定义域内的任意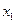 、
、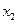 ,都有
,都有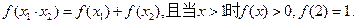
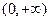 上是增函数;
上是增函数;
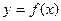 ,满足
,满足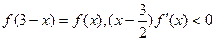 ,若
,若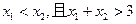 则有 ( )
则有 ( )