题目内容
设函数f(x)=
,若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
|
A.(
| B.(
| C.(
| D.(
|
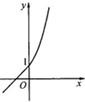
函数f(x)=
的图象,如图,

不妨设x1<x2<x3,则x2,x3关于直线x=3对称,故x2+x3=6,
且x1满足-
<x1<0;
则x1+x2+x3的取值范围是:-
+6<x1+x2+x3<0+6;
即x1+x2+x3∈(
,6).
故选D
|

不妨设x1<x2<x3,则x2,x3关于直线x=3对称,故x2+x3=6,
且x1满足-
| 7 |
| 3 |
则x1+x2+x3的取值范围是:-
| 7 |
| 3 |
即x1+x2+x3∈(
| 11 |
| 3 |
故选D

练习册系列答案
相关题目
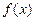 ,
,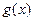 分别由下表给出
分别由下表给出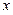
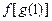 的值为 ;满足
的值为 ;满足 的
的
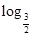
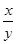 的值.
的值.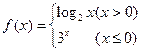 ,则
,则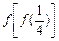 的值为_____________.
的值为_____________.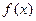 对于任意实数
对于任意实数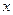 满足条件
满足条件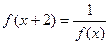 ,若
,若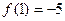 ,则
,则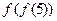 = 。
= 。