题目内容
设函数g(x)=x2-2,f(x)=
,则f(x)的值域是( )
|
A.[-
| B.[0,+∞) | C.[-
| D.[-
|
x<g(x),即 x<x2-2,即 x<-1 或 x>2. x≥g(x),即-1≤x≤2.
由题意 f(x)=
=
=
,
所以当x∈(-∞,-1)∪(2,+∞)时,由二次函数的性质可得 f(x)∈(2,+∞);
x∈[-1,2]时,由二次函数的性质可得f(x)∈[-
,0],
故选 D.
由题意 f(x)=
|
|
=
|
所以当x∈(-∞,-1)∪(2,+∞)时,由二次函数的性质可得 f(x)∈(2,+∞);
x∈[-1,2]时,由二次函数的性质可得f(x)∈[-
| 9 |
| 4 |
故选 D.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 的定义域为R,并满足以下条件:①对任意
的定义域为R,并满足以下条件:①对任意 ,有
,有 ;
; 、
、 ,有
,有 ;③
;③ 则
则 的值; (4分)
的值; (4分)  ,求证:
,求证:
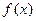 的定义域为
的定义域为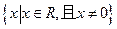 对定义域内的任意
对定义域内的任意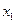 、
、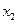 ,都有
,都有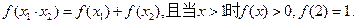
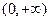 上是增函数;
上是增函数;
 ,函数
,函数
 .
. 的单调性.
的单调性.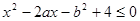 恰有一解,则
恰有一解,则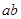 的最大值为______.
的最大值为______.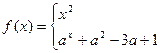
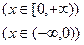 在区间
在区间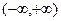 是增函数,则常数a的取值范围是
是增函数,则常数a的取值范围是