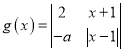题目内容
【题目】已知![]() (其中
(其中![]() ).
).
(1)当![]() 时,计算
时,计算![]() 及
及![]() ;
;
(2)记![]() ,试比较
,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
【答案】(1)![]() ;(2)答案不唯一,见解析
;(2)答案不唯一,见解析
【解析】
(1)采用赋值法,令![]() ,计算
,计算![]() ,然后令
,然后令![]() 和
和![]() ,求
,求![]() 的值;
的值;
(2)由(1)知,![]() ,比较
,比较![]() 与
与![]() 的大小,利用数学归纳法证明.
的大小,利用数学归纳法证明.
(1)当![]() 时,取
时,取![]() ,得
,得![]() ,
,
取![]() 时,得
时,得![]() ,……①
,……①
取![]() 时,得
时,得![]() ,……②
,……②
将①-②得:![]() ,
,
所以![]() .
.
(2)由(1)可知![]() ,
,
要比较![]() 与
与![]() 的大小,只要比较
的大小,只要比较![]() 与
与![]() ,
,
只要比较![]() 与
与![]() ,
,
当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,所以左边
,所以左边![]() 右边;
右边;
当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,所以左边
,所以左边![]() 右边;
右边;
当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,所以左边
,所以左边![]() 右边;
右边;
当![]() 时,左边
时,左边![]() ,右边=
,右边=![]() ,所以左边
,所以左边![]() 右边;
右边;
猜想当![]() 时,左边
时,左边![]() 右边,即
右边,即![]() .
.
下面用数学归纳法证明:
①当![]() 时已证;
时已证;
②假设当![]() 时
时![]() 成立,
成立,
则当![]() 时,左边
时,左边![]()
![]() ,
,
因为![]()
![]()
![]() ,
,
所以![]() ,即当
,即当![]() 时不等式也成立.
时不等式也成立.
所以![]() 对
对![]() 的一切正整数都成立.
的一切正整数都成立.
综上所述:当![]() 或
或![]() 时,
时,![]() ,
,
当![]() 或
或![]() 时
时![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目