题目内容
【题目】设函数![]() .
.
(1)若![]() ,解不等式
,解不等式![]() ;
;
(2)若当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设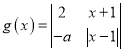 ,若存在
,若存在![]() 使不等式
使不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用零点分段讨论可求不等式的解.
(2)![]() 的解为
的解为![]() ,在该条件下
,在该条件下![]() 恒成立即为
恒成立即为![]() 恒成立,参变分离后可求实数
恒成立,参变分离后可求实数![]() 的取值范围.
的取值范围.
(3)![]() 有解即为
有解即为![]() 有解,利用绝对值不等式可求
有解,利用绝对值不等式可求![]() 的最小值,从而可得
的最小值,从而可得![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() 即为
即为![]() .
.
当![]() 时,不等式可化为
时,不等式可化为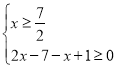 ,故
,故![]() ;
;
当![]() 时,不等式可化为
时,不等式可化为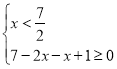 ,故
,故![]() .
.
综上,![]() 的解为
的解为![]() .
.
(2)![]() 的解为
的解为![]() ,
,
当![]() 时,有
时,有![]() ,
,
因为不等式![]() 恒成立,故
恒成立,故![]() 即
即![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上恒成立,而
上恒成立,而![]() 在
在![]() 上总成立,
上总成立,
所以![]() 即
即![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.
(3)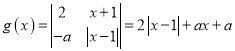 ,
,
![]() 等价于
等价于![]() ,
,
即![]() 在
在![]() 上有解.
上有解.
令![]() ,
,
由绝对值不等式有![]() ,
,
所以![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立,
成立,
所以![]() ,故
,故![]() 即
即![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】近年来,人们的支付方式发生了巨大转变,使用移动支付购买商品已成为一部分人的消费习惯.某企业为了解该企业员工![]() 、
、![]() 两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况.发现样本中
两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况.发现样本中![]() ,
,![]() 两种支付方式都没有使用过的有5人;使用了
两种支付方式都没有使用过的有5人;使用了![]() 、
、![]() 两种方式支付的员工,支付金额和相应人数分布如下:
两种方式支付的员工,支付金额和相应人数分布如下:
支付金额(元) 支付方式 |
|
| 大于2000 |
使用 | 18人 | 29人 | 23人 |
使用 | 10人 | 24人 | 21人 |
依据以上数据估算:若从该公司随机抽取1名员工,则该员工在该月![]() 、
、![]() 两种支付方式都使用过的概率为______.
两种支付方式都使用过的概率为______.