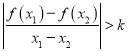题目内容

【题目】已知在平面直角坐标系中， 是坐标原点，动圆经过点，且与直线相切.

（1）求动圆圆心的轨迹方程；

（2）过的直线交曲线于两点，过作曲线的切线，直线交于点，求的面积的最小值.

【答案】（1）（2）4

【解析】试题分析: (1)由直接法求出轨迹方程; (2)假设 以及直线 ,联立直线与抛物线方程,求出 表达式,求出点M到直线 的距离,由 ,再算出最小值.

试题解析: (1)设动圆圆心 ,由已知条件有

（2）设，直线

将代入中得

所以， ，

得切线：

点睛: 本题主要考查轨迹方程的求法和直线与抛物线相交时求三角形的面积, 属于中档题. 解题思路: (1)利用直线与圆相切时,圆心到直线的距离等于半径, 求出圆心的轨迹方程; (2)联立直线与抛物线方程, 由韦达定理求出两根之和,两根之积,求出,由导数几何意义,求出切线 的斜率,求出的交点M, 由面积 ,算出最小值.

练习册系列答案
相关题目

【题目】设函数， (a>0且a≠1)是定义域为R的奇函数．

(Ⅰ) 求的值

（Ⅱ）若，试求不等式的解集；

（Ⅲ）若，且，求在上的最小值。

【题目】在平面直角坐标系中，已知椭圆（），圆（），若圆的一条切线与椭圆相交于两点.

（1）当， 时，若点都在坐标轴的正半轴上，求椭圆的方程；

（2）若以为直径的圆经过坐标原点，探究是否满足，并说明理由.

【题目】(2015·广东卷)若直线l1和l2是异面直线，l1在平面α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是(　　)

A. l与l1，l2都不相交

B. l与l1，l2都相交

C. l至多与l1，l2中的一条相交

D. l至少与l1，l2中的一条相交

【题目】已知椭圆： （）的焦距为，点在上.

（Ⅰ）求椭圆的方程；

（Ⅱ）设点在上，点的轨迹为曲线，过原点作直线与曲线交于、两点，点，证明： 为定值，并求出定值.

【题目】下列命题正确的是__________．（写出所有正确命题的序号）

①已知，“且”是“”的充要条件；

②已知平面向量，“且”是“”的必要不充分条件；

③已知，“”是“”的充分不必要条件；

④命题：“，使且”的否定为：“，都有且”

【题目】已知函数f（x）=x2-3x+lnx．

（Ⅰ）求函数f（x）的极值；

（Ⅱ）若对于任意的x1，x2∈（1，+∞），x1≠x2，都有恒成立，求实数k的取值范围．

【题目】已知椭圆和直线： ，椭圆的离心率，坐标原点到直线的距离为.

（Ⅰ）求椭圆的方程；

（Ⅱ）已知定点，若直线过点且与椭圆相交于两点，试判断是否存在直线，使以为直径的圆过点？若存在，求出直线的方程；若不存在，请说明理由.

【题目】已知函数 ()在定义域内仅有唯一零点．

（1）若对，不等式恒成立，求实数的最大值；

（2）设函数，对于， ，且，求证： ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网