题目内容
【题目】(2015·广东卷)若直线l1和l2是异面直线，l1在平面α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是( )
A. l与l1，l2都不相交
B. l与l1，l2都相交
C. l至多与l1，l2中的一条相交
D. l至少与l1，l2中的一条相交
【答案】D
【解析】试题分析：可以画出图形来说明l与l1，l2的位置关系，从而可判断出A，B，C是错误的，而对于D，可假设不正确，这样l便和l1，l2都不相交，这样可退出和l1，l2异面矛盾，这样便说明D正确．
解：A．l与l1，l2可以相交，如图：
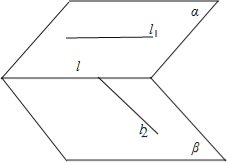∴该选项错误；
B．l可以和l1，l2中的一个平行，如上图，∴该选项错误；
C．l可以和l1，l2都相交，如下图：
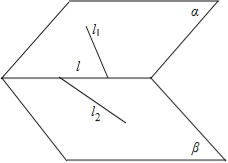，∴该选项错误；
D．“l至少与l1，l2中的一条相交”正确，假如l和l1，l2都不相交；
∵l和l1，l2都共面；
∴l和l1，l2都平行；
∴l1∥l2，l1和l2共面，这样便不符合已知的l1和l2异面；
∴该选项正确．
故选D．
练习册系列答案
备战中考寒假系列答案
相关题目
