题目内容
14.已知数列{an}的前n项和为Sn,且Sn=n(n+1).(1)求数列{an}的通项公式an;
(Ⅱ)数列{bn}的通项公式bn=$\frac{1}{{a}_{n}•{a}_{n+2}}$,其前n项和为Tn,求证:${T_n}<\frac{3}{16}$.
分析 (1)n=1时,a1=S1,当n≥2时,an=Sn-Sn-1即可得出.
(2)由(1)可知bn=$\frac{1}{2n•2(n+2)}$=$\frac{1}{8}(\frac{1}{n}-\frac{1}{n+2})$,利用“裂项求和”与“放缩法”即可得出.
解答 (1)解:n=1时,a1=S1=2,
当n≥2时,an=Sn-Sn-1=n(n+1)-n(n-1)=2n,
经检验n=1时成立,
综上可得:an=2n.
(2)证明:由(1)可知bn=$\frac{1}{{a}_{n}•{a}_{n+2}}$=$\frac{1}{2n•2(n+2)}$=$\frac{1}{8}(\frac{1}{n}-\frac{1}{n+2})$,
∴Tn=$\frac{1}{8}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})+(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{8}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$<$\frac{1}{8}×\frac{3}{2}$=$\frac{3}{16}$.
∴${T_n}<\frac{3}{16}$.
点评 本题考查了递推式的应用、“裂项求和”、“放缩法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.如图所示,程序框图(算法流程图)的输出结果为( )
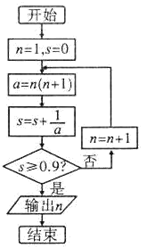

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
9.椭圆ax2+by2=1与直线y=1-x交于A、B两点,过原点与线段AB中点的直线的斜率为$\frac{\sqrt{3}}{2}$,则$\frac{b}{a}$值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{27}$ |
6.已知抛物线y2=4x上两个动点B、C和点A(1,2),且∠BAC=90°,则动直线BC必过定点( )
| A. | (2,5) | B. | (-2,5) | C. | (5,-2) | D. | (5,2) |
3. 如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
 如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )| A. | 甲 | B. | 乙 | C. | 甲、乙相等 | D. | 无法确定 |
4.已知双曲线的左、右焦点分别为F1,F2,在左支上过F1的弦AB的长为10,若2a=16,则△ABF2的周长是( )
| A. | 32 | B. | 36 | C. | 42 | D. | 52 |