题目内容
7.在三棱柱ABC-A1B1C1中,△ABC为正三角形,AA1⊥底面ABC,E是AB的中点,F是BC1的中点.下列命题正确的是①②③⑤(写出所有正确命题的编号).①EF∥平面ACC1A1;
②平面CEF⊥平面 ABB1A1;
③平面CEF截该三棱柱所得大小两部分的体积比为11:1;
④若该三棱柱有内切球,则AB=$\sqrt{3}$BB1;
⑤若BB1上有唯一点G,使得A1G⊥CG,则BB1=$\sqrt{2}$AB.
分析 由条件利用直线和平面平行的判定定理,可得①正确;由条件利用平面和平面平行的判定定理可得②正确;用分割法求几何体的体积,可得③正确;设内切球的半径为r,则棱AA1 到平面BCC1B1的距离等于2r,且也等于原棱柱的高,求得$\frac{\sqrt{3}}{2}$AB=BB1,可得④不正确;根据以A1C 为直径的球和棱BB1相切,求得BB1=$\sqrt{2}$AB,故⑤正确,从而得出结论.
解答 解:对于①,由题意可得,EF为△BAC1的中位线,故有EF∥AC1,而AC1?平面 ABB1A1,EF?平面 ABB1A1,∴EF∥平面ACC1A1,故①正确.
对于②,在直三棱柱ABC-A1B1C1中,ABB1A1⊥平面ABC,平面 ABB1A1∩ABC=AB,CE⊥AB,CE?平面ABC,∴CE⊥平面 ABB1A1.
再根据CE平面CEF,可得平面CEF⊥平面 ABB1A1,故②正确.
对于③,平面CEF截该三棱柱所得大小两部分,设原棱柱的高为x,底面积为s,则较小的部分为三棱锥F-BCE,它的体积为 $\frac{1}{3}$S△BCE•$\frac{1}{2}$x=$\frac{1}{3}$•$\frac{1}{2}$s•$\frac{x}{2}$,
故较大部分的体积sx=$\frac{1}{3}$•$\frac{1}{2}$s•$\frac{x}{2}$=$\frac{11}{12}$sx,故平面CEF截该三棱柱所得大小两部分的体积比为11:1,故③正确.
对于④,若该三棱柱有内切球,设内切球的半径为r,则棱AA1 到平面BCC1B1的距离等于2r,且原棱柱的高也都等于2r,
故有2r=$\frac{\sqrt{3}}{2}$AB=BB1,故④不正确.
对于⑤,若BB1上有唯一点G,使得A1G⊥CG,则以A1C 为直径的球和棱BB1相切,故求得半径$\frac{{A}_{1}C}{2}$=$\frac{\sqrt{3}}{2}$AB,
即 $\frac{\sqrt{{{BB}_{1}}^{2}{+AB}^{2}}}{2}$=$\frac{\sqrt{3}}{2}$AB,化简可得BB1=$\sqrt{2}$AB,故⑤正确.
故答案为:①②③⑤.
点评 本题主要考查棱柱的结构特征,直线和平面平行、垂直的判定、性质,平面和平面平行的判定定理,用分割法求几何体的体积,以及点到平面的距离、直线到平面的距离的转化,属于中档题.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案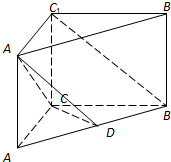 如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.
如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.(1)证明:BC1∥面A1CD;
(2)求面A1CD与面A1C1CA所成的锐二面角的余弦值.
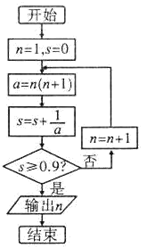
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
| A. | 6个 | B. | 4个 | C. | 3个 | D. | 2个 |
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 5.15 | B. | 5.20 | C. | 5.25 | D. | 5.30 |