题目内容
3.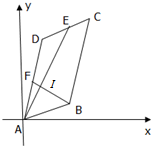 如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)
如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)(1)求顶点D的坐标;
(2)若$\overrightarrow{DE}$=2$\overrightarrow{EC}$,F为AD的中点,求AE与BF的交点I的坐标.
分析 (1)设D(x,y),则$\overrightarrow{AB}$=(4,1)=$\overrightarrow{DC}$=(6-x,8-y),即可求顶点D的坐标;
(2)设I(a,b),则由题意,F(1,3.5),E($\frac{14}{3}$,$\frac{23}{3}$),利用向量共线,建立方程,即可求AE与BF的交点I的坐标.
解答 解:(1)设D(x,y),则$\overrightarrow{AB}$=(4,1)=$\overrightarrow{DC}$=(6-x,8-y),
∴6-x=4,8-y=1,
∴x=2,y=7,即D(2,7);
(2)设I(a,b),则
由题意,F(1,3.5),E($\frac{14}{3}$,$\frac{23}{3}$),
∴$\overrightarrow{AI}$=(a,b),$\overrightarrow{AE}$=($\frac{14}{3}$,$\frac{23}{3}$),
∴14b=23a.
$\overrightarrow{BI}$=(a-4,b-1),$\overrightarrow{BF}$=(-3,2.5),
∴2.5(a-4)=-3(b-1),
∴a=$\frac{52}{79}$,b=$\frac{598}{553}$,
∴I($\frac{52}{79}$,$\frac{598}{553}$).
点评 本题考查向量知识的运用,考查学生分析解决问题的能力,正确求向量是关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
13.对于x∈(0,$\frac{π}{2}$),不等式$\frac{1}{si{n}^{2}x}$+$\frac{p}{co{s}^{2}x}$≥16恒成立,则正数p的取值范围为( )
| A. | (-∞-9) | B. | (-9,9] | C. | (-∞,9] | D. | [9,+∞) |
18.某工厂对同时生产某件产品的件数x(单位:件)与所用时间y(单位:小时)进行了测验.测验结果如下表所示:
(1)求出y与x的线性回归方程$\widehat{y}$=bx+a;
(2)试预测同时生产20件该产品需要多少小时?
(附:线性回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}-b\overline{x}$)
| 件数x(件) | 11 | 12 | 13 |
| 时间y(小时) | 25 | 26 | 30 |
(2)试预测同时生产20件该产品需要多少小时?
(附:线性回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}-b\overline{x}$)
13.圆(x+1)2+(y+2)2=8上与直线x+y+1=0距离等于$\sqrt{3}$的点共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |