题目内容
12.若椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$经过点P(0,$\sqrt{3}$),且椭圆的长轴长是焦距的两倍,则a=2.分析 根据椭圆中长轴、短轴、焦距的关系,以及已知条件,计算即可.
解答 解:∵椭圆C经过点P(0,$\sqrt{3}$),∴$0+\frac{{\sqrt{3}}^{2}}{{b}^{2}}=1$,
∵椭圆的长轴长是焦距的两倍,∴$\frac{2a}{2c}=2$,
又∵c2=a2-b2,
∴$(\frac{a}{2})^{2}={a}^{2}-{(\sqrt{3})}^{2}$,
解得a=2或-2(舍),
故答案为:2.
点评 本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意积累解题方法,属于基础题.

练习册系列答案
相关题目
2.已知椭圆$\frac{{x}^{2}}{4}+{y}^{2}=1$的焦点为F1,F2,在长轴A1A2上任取一点M,过M作垂直于A1A2的直线交椭圆于点P,则∠F1PF2为钝角的概率为( )
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
17.在长方体ABCD-A′B′C′D′中,下列正确的是( )
| A. | 平面ABCD∥平面ABB′A′ | B. | 平面ABCD∥平面ADD′A′ | ||
| C. | 平面ABCD∥平面CDD′C′ | D. | 平面ABCD∥平面A′B′C′D′ |
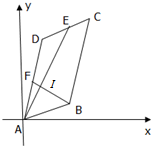 如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)
如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)