题目内容
8.已知数列{an}的首项a1=1,且满足an-1-an=anan-1(n≥2),则a1a2+a2a3+…+a2014a2015=$\frac{2014}{2015}$.分析 由an-1-an=anan-1(n≥2),变形后得到数列{$\frac{1}{{a}_{n}}$}是等差数列,从而求出an,再计算即可.
解答 解:∵an-1-an=anan-1(n≥2),
∴$\frac{{a}_{n-1}-{a}_{n}}{{a}_{n}{a}_{n-1}}$=$\frac{{a}_{n}{a}_{n-1}}{{a}_{n}{a}_{n-1}}$,化简得$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=1,
又a1=1,即$\frac{1}{{a}_{1}}$=1,
所以数列{$\frac{1}{{a}_{n}}$}是以1为首项,1为公差的等差数列,
从而$\frac{1}{{a}_{n}}$=1+n-1=n,即an=$\frac{1}{n}$,
所以a1a2+a2a3+…+a2014a2015
=a1-a2+a2-a3+…+a2014-a2015
=a1-a2015
=$1-\frac{1}{2015}$
=$\frac{2014}{2015}$,
故答案为:$\frac{2014}{2015}$.
点评 本题考查递推公式,对不等式灵活的进行变形是解题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
13.已知离心率为e的双曲线和离心率为$\frac{{\sqrt{2}}}{2}$的椭圆有相同的焦点F1,F2,P是两曲线的一个公共点,若∠F1PF2=$\frac{π}{3}$,则e等于( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 3 |
17.在长方体ABCD-A′B′C′D′中,下列正确的是( )
| A. | 平面ABCD∥平面ABB′A′ | B. | 平面ABCD∥平面ADD′A′ | ||
| C. | 平面ABCD∥平面CDD′C′ | D. | 平面ABCD∥平面A′B′C′D′ |
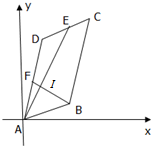 如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)
如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)