题目内容
13.圆(x+1)2+(y+2)2=8上与直线x+y+1=0距离等于$\sqrt{3}$的点共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先确定圆的圆心坐标与半径,再求出圆心到直线x+y+1=0的距离,从而可得结论.
解答 解:由题意,圆心坐标为(-1,-2),半径为2$\sqrt{2}$.
∴圆心到直线x+y+1=0的距离为d=$\frac{|-1-2+1|}{\sqrt{2}}$=$\sqrt{2}$.
∴圆(x+1)2+(y+2)2=8上与直线x+y+1=0相交,且圆(x+1)2+(y+2)2=8上与直线x+y+1=0的距离等于$\sqrt{3}$的点共有2个
故选:B.
点评 本题考查的重点是直线与圆的位置关系,解题的关键是求出圆心到直线x+y+1=0的距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知圆C:x2+y2=1,点M(t,2),若C上存在两点A,B满足$\overrightarrow{MA}$=$\overrightarrow{AB}$,则t的取值范围是( )
| A. | [-2,2] | B. | [-3,3] | C. | [-$\sqrt{5}$,$\sqrt{5}$] | D. | [-5,5] |
18.若f′(x0)=-$\frac{1}{2}$,则$\underset{lim}{h→0}$$\frac{f({x}_{0})-f({x}_{0}-3h)}{h}$=$-\frac{3}{2}$.
5.已知集合A={x|x2≥4},B={y|y=|tanx|},则(∁RA)∩B=( )
| A. | (-∞,2] | B. | (0,+∞) | C. | (0,2) | D. | [0,2) |
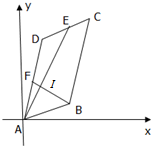 如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)
如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)