题目内容
15.已知:在数列{an},前n项和Sn=$\frac{3}{2}$n2+$\frac{7}{2}$n.(1)求an;
(2)将{an}中的第2项,第4项,…,第2n项按原来的顺序排成一个新数列,求此数列的前n项和Gn.
分析 (1)利用递推式即可得出;
(2)利用等比数列的前n项和公式即可得出.
解答 解:(1)∵Sn=$\frac{3}{2}$n2+$\frac{7}{2}$n,
∴当n=1时,a1=$\frac{3}{2}+\frac{7}{2}$=5,
当n≥2时,an=Sn-Sn-1=$\frac{3}{2}$n2+$\frac{7}{2}$n-$[\frac{3}{2}(n-1)^{2}+\frac{7}{2}(n-1)]$=3n+2.
当n=1时上式成立,∴an=3n+2(n∈N*).
(2)${a}_{{2}^{n}}$=3×2n+2.
∴此数列的前n项和Gn=3×(2+22+23+…+2n)+2n
=$3×\frac{2({2}^{n}-1)}{2-1}$
=3×2n+1-6+2n.
点评 本题考查了递推式的应用、等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.对于定义在实数集R上的函数f(x),如果存在实数x0,使f(x0)=x0,那么x0叫做函数f(x)的一个好点.已知函数f(x)=x2+2ax+1不存在好点,那么a的取值范围是( )
| A. | (-$\frac{1}{2}$,$\frac{3}{2}$) | B. | (-$\frac{3}{2}$,$\frac{1}{2}$) | C. | (-1,1) | D. | (-∞,1)∪(1,+∞) |
10.若a=${∫}_{0}^{π}$sinxdx,则(x+$\frac{1}{x}$)(ax-1)5的展开式中的常数项为( )
| A. | 10 | B. | 20 | C. | -10 | D. | -20 |
5.已知集合A={x|x2≥4},B={y|y=|tanx|},则(∁RA)∩B=( )
| A. | (-∞,2] | B. | (0,+∞) | C. | (0,2) | D. | [0,2) |
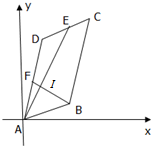 如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)
如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)