题目内容
11.已知向量$\overrightarrow{OA}$=(3,4),$\overrightarrow{OB}$=(-9,2),$\overrightarrow{OC}$=(1,7).(1)分别求线段BC、AC的中点E、F坐标;
(2)求AE,BF的交点M的坐标;
(3)在直线AB上求一点P,使|$\overrightarrow{AP}$|=$\frac{1}{3}$|$\overrightarrow{AB}$|.
分析 (1)先求出点A,B,C的坐标,根据中点坐标公式即可求出E,F点的坐标;
(2)先求出直线AE,BF的方程,然后解这两个方程形成的方程组即得M点坐标;
(3)根据已知即得$\overrightarrow{AP}=±\frac{1}{3}\overrightarrow{AB}$,设P(x0,y0),带入A,B点坐标,即可得到关于x0,y0的二元一次方程组,求解方程组即得P点坐标.
解答 解:(1)根据已知得:A(3,4),B(-9,2),C(1,7);
根据中点坐标公式得,E(-4,$\frac{9}{2}$),F(2,$\frac{11}{2}$);
(2)直线AE的方程为:y-4=$-\frac{1}{14}$(x-3),直线BF的方程为:y-2=$\frac{7}{22}$(x+9);
联立这两方程解方程组得,x=$-\frac{5}{3}$,y=$\frac{13}{3}$;
∴M($-\frac{5}{3},\frac{13}{3}$);
(3)$\overrightarrow{AB}=(-12,-2)$,点P在AB上,且$|\overrightarrow{AP}|=\frac{1}{3}|\overrightarrow{AB}|$;
∴$\overrightarrow{AP}=±\frac{1}{3}\overrightarrow{AB}$,设P(x0,y0),$\overrightarrow{AP}=({x}_{0}-3,{y}_{0}-4)$;
∴$({x}_{0}-3,{y}_{0}-4)=±\frac{1}{3}(-12,-2)$;
∴$\left\{\begin{array}{l}{{x}_{0}=-1}\\{{y}_{0}=\frac{10}{3}}\end{array}\right.,或\left\{\begin{array}{l}{{x}_{0}=7}\\{{y}_{0}=\frac{14}{3}}\end{array}\right.$;
∴$P(-1,\frac{10}{3}),或P(7,\frac{14}{3})$.
点评 考查向量的起点是原点时,向量坐标和终点坐标的关系,中点坐标公式,直线的点斜式方程,以及由两点坐标求直线斜率,共线向量基本定理,数乘的几何意义.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
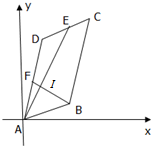 如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)
如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)