题目内容
18.某工厂对同时生产某件产品的件数x(单位:件)与所用时间y(单位:小时)进行了测验.测验结果如下表所示:| 件数x(件) | 11 | 12 | 13 |
| 时间y(小时) | 25 | 26 | 30 |
(2)试预测同时生产20件该产品需要多少小时?
(附:线性回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}-b\overline{x}$)
分析 (1)计算系数b,a,即可得到线性回归方程;
(2)利用线性回归方程,令x=20,可得y.
解答 解:(1)$\overline{x}$=$\frac{11+12+13}{3}$=12,$\overline{y}$=$\frac{25+26+30}{3}$=27,
∴b=$\frac{(11-12)(25-27)+(12-12)(26-27)+(13-12)(30-27)}{(11-12)^{2}+(12-12)^{2}+(13-12)^{2}}$=2.5,a=-3
∴y=2.5x-3;
(2)x=20,y=2.5×20-3=47.
点评 本题考查线性回归知识,考查学生的计算能力,属于中档题,正确计算是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.已知正方体ABCD-A1B1C1D1的棱长为l,动点P在正方体表面上且满足|PA|=|PC1|,则动点P的轨迹长度为( )
| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 6 |
10.若a=${∫}_{0}^{π}$sinxdx,则(x+$\frac{1}{x}$)(ax-1)5的展开式中的常数项为( )
| A. | 10 | B. | 20 | C. | -10 | D. | -20 |
8.已知圆C:x2+y2=1,点M(t,2),若C上存在两点A,B满足$\overrightarrow{MA}$=$\overrightarrow{AB}$,则t的取值范围是( )
| A. | [-2,2] | B. | [-3,3] | C. | [-$\sqrt{5}$,$\sqrt{5}$] | D. | [-5,5] |
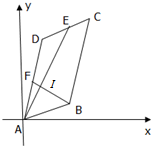 如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)
如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)