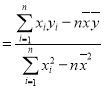题目内容
【题目】如图所示的立体图形中,![]() ,
,![]() .
.
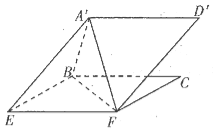
(Ⅰ)证明:![]()
![]()
![]() ;
;
(Ⅱ)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)要证![]()
![]()
![]() ,只需证
,只需证![]() 平面
平面![]() ,要证
,要证![]() 平面
平面![]() ,只需证明
,只需证明![]() 垂直于平面
垂直于平面![]() 两条相交直线即可,取
两条相交直线即可,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,由题意可得
,由题意可得![]()
![]() ,
,
再写出证明的过程即可
(Ⅱ)由题目中的垂直关系建立以![]() 为原点,直线
为原点,直线![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴
轴
建立空间直角坐标系![]() ,写出需要的点的坐标,再求得平面
,写出需要的点的坐标,再求得平面![]() 的一个法向量,易知
的一个法向量,易知![]() 是平面
是平面![]() 的一个法向量,求出两法向量的夹角的余弦值,由于因为二面角
的一个法向量,求出两法向量的夹角的余弦值,由于因为二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.
试题解析:(Ⅰ)证明:在图2中取![]() 的中点
的中点![]() ,
,
连接![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]()
![]()
![]() .
.
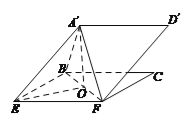
(Ⅱ)由(Ⅰ)知![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,
,![]() ,
,
所以![]() ,
,
以![]() 为原点,直线
为原点,直线![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴
轴
建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,可求得平面
,可求得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
易知![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
所以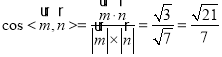 ,
,
因为二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
(1)从该单位中任取2人,此2人中年薪收入高于5万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(2)已知员工年薪收入![]() 与工作所限
与工作所限![]() 成正相关关系,某员工工作第一年至第四年的年薪如下表:
成正相关关系,某员工工作第一年至第四年的年薪如下表:
工作年限 | 1 | 2 | 3 | 4 |
年薪(万元) | 3.0 | 4.2 | 5.6 | 7.2 |
预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式和参考数据分别为:
中系数计算公式和参考数据分别为:
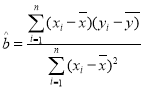 ,
,![]() ,其中
,其中![]() 为样本均值,
为样本均值,![]() ,
,![]() ,(
,(![]() )
)