ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥Μ·ΙΛ≥ßΫϋΤΎ“Σ…ζ≤ζ“Μ≈ζΜ·ΙΛ ‘ΦΝΘ§Ψ≠ –≥ΓΒς•ΥΒΟ÷ΣΘ§…ζ≤ζ’β≈ζ ‘ΦΝ≥ßΦ“ΒΡ…ζ≤ζ≥…±Ψ”–“‘œ¬»ΐΗω≤ΩΖ÷ΘΚΔΌ…ζ≤ζ![]() ΒΞΈΜ ‘ΦΝ–η“Σ‘≠ΝœΖ―
ΒΞΈΜ ‘ΦΝ–η“Σ‘≠ΝœΖ―![]() ‘Σ; ΔΎ÷ßΗΕΥυ”–÷ΑΙΛΒΡΙΛΉ ΉήΕν”…
‘Σ; ΔΎ÷ßΗΕΥυ”–÷ΑΙΛΒΡΙΛΉ ΉήΕν”…![]() ‘ΣΒΡΜυ±ΨΙΛΉ ΚΆΟΩ…ζ≤ζ
‘ΣΒΡΜυ±ΨΙΛΉ ΚΆΟΩ…ζ≤ζ![]() ΒΞΈΜ ‘ΦΝ≤ΙΌNΥυ”–÷ΑΙΛ
ΒΞΈΜ ‘ΦΝ≤ΙΌNΥυ”–÷ΑΙΛ![]() ‘ΣΉι≥…; ΔέΚσ–χ±Θ―χΒΡΤΫΨυΖ―”Ο «ΟΩΒΞΈΜ
‘ΣΉι≥…; ΔέΚσ–χ±Θ―χΒΡΤΫΨυΖ―”Ο «ΟΩΒΞΈΜ![]() ‘ΣΘ® ‘ΦΝΒΡΉή≤ζΝΩΈΣ
‘ΣΘ® ‘ΦΝΒΡΉή≤ζΝΩΈΣ![]() ΒΞΈΜ,
ΒΞΈΜ,![]() Θ©.
Θ©.
Θ®1Θ©Α―…ζ≤ζΟΩΒΞΈΜ ‘ΦΝΒΡ≥…±Ψ±μ ΨΈΣ![]() ΒΡΚ· ΐΙΊœΒ
ΒΡΚ· ΐΙΊœΒ![]() ,≤Δ«σ≥ω
,≤Δ«σ≥ω![]() ΒΡΉν–Γ÷Β;
ΒΡΉν–Γ÷Β;
Θ®2Θ©»γΙϊ≤ζΤΖ»Ϊ≤Ω¬τ≥ω,Ψί≤βΥψœζ έν~![]() Θ®‘ΣΘ©ΙΊ”Ύ≤ζΝΩ
Θ®‘ΣΘ©ΙΊ”Ύ≤ζΝΩ![]() Θ®ΒΞΈΜΘ©ΒΡΚ· ΐΙΊœΒΈΣ
Θ®ΒΞΈΜΘ©ΒΡΚ· ΐΙΊœΒΈΣ![]() , ‘Έ ΘΚΒ±≤ζΝΩΈΣΕύ…Ό ±…ζ≤ζ’β≈ζ ‘ΦΝΒΡάϊ»σΉνΗΏ?
, ‘Έ ΘΚΒ±≤ζΝΩΈΣΕύ…Ό ±…ζ≤ζ’β≈ζ ‘ΦΝΒΡάϊ»σΉνΗΏ?
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() Ήν–Γ÷Β
Ήν–Γ÷Β![]() ‘ΣΘ®2Θ©
‘ΣΘ®2Θ©![]()
ΓΨΫβΈωΓΩ
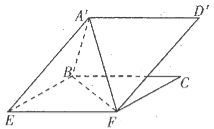
‘ΧβΖ÷ΈωΘΚΘ®1Θ©≥…±ΨΖ÷»ΐ≤ΩΖ÷Θ§“Μ «‘≠ΝœΖ―![]() Θ§Εΰ «ΙΛΉ ΉήΕν
Θ§Εΰ «ΙΛΉ ΉήΕν![]() Θ§»ΐ «±Θ―χΒΡΖ―”Ο
Θ§»ΐ «±Θ―χΒΡΖ―”Ο![]() Θ§“ρ¥ΥΟΩΒΞΈΜ≥…±ΨΈΣ
Θ§“ρ¥ΥΟΩΒΞΈΜ≥…±ΨΈΣ![]() Θ§Ε®“ε”ρΈΣ
Θ§Ε®“ε”ρΈΣ![]() Θ§ΗυΨίΜυ±Ψ≤ΜΒ» Ϋ«σΉν÷ΒΘ®2Θ©άϊ»σΈΣœζ έΕνΦθ»Ξ≥…±Ψ
Θ§ΗυΨίΜυ±Ψ≤ΜΒ» Ϋ«σΉν÷ΒΘ®2Θ©άϊ»σΈΣœζ έΕνΦθ»Ξ≥…±Ψ![]() Θ§άϊ”ΟΒΦ ΐ«σΤδΉν÷ΒΘΚΦΪ÷ΒΒψ“≤ «Ήν÷ΒΒψ
Θ§άϊ”ΟΒΦ ΐ«σΤδΉν÷ΒΘΚΦΪ÷ΒΒψ“≤ «Ήν÷ΒΒψ
‘ΧβΫβΈωΘΚΘ®1Θ©“ρΈΣ ‘ΦΝΒΡΉή≤ζΝΩΈΣ![]() ΒΞΈΜ, ‘ρ ‘ΦΝ–η“Σ‘≠ΝœΖ―
ΒΞΈΜ, ‘ρ ‘ΦΝ–η“Σ‘≠ΝœΖ―![]() ‘Σ, ÷ΑΙΛΒΡΙΛΉ ΉήΕν
‘Σ, ÷ΑΙΛΒΡΙΛΉ ΉήΕν![]() ‘Σ, Κσ–χ±Θ―χΒΡΖ―”Ο «ΟΩΒΞΈΜ
‘Σ, Κσ–χ±Θ―χΒΡΖ―”Ο «ΟΩΒΞΈΜ![]() ‘Σ,
‘Σ, ![]() ,
,![]() ,Β±«“ΫωΒ±
,Β±«“ΫωΒ±![]() ,Φ¥
,Φ¥![]() ±»ΓΒ»Κ≈,
±»ΓΒ»Κ≈,![]() ±,
±,![]() Ήν–Γ÷Β
Ήν–Γ÷Β![]() ‘Σ, Φ¥…ζ≤ζΟΩΒΞΈΜ ‘ΦΝΒΡ≥…±ΨΉνΒΆΈΣ
‘Σ, Φ¥…ζ≤ζΟΩΒΞΈΜ ‘ΦΝΒΡ≥…±ΨΉνΒΆΈΣ![]() ‘Σ.
‘Σ.
Θ®2Θ©…ζ≤ζ’β≈ζ ‘ΦΝΒΡάϊ»σ![]()
![]() ,
,![]() ,Νν
,Νν![]() ,ΒΟ
,ΒΟ![]() Μρ
Μρ![]() Θ®…α»ΞΘ©,
Θ®…α»ΞΘ©,![]() Β±
Β±![]() ±,
±,![]() , Β±
, Β±![]() ±,
±,![]() ,
,![]() ±, Κ· ΐ»ΓΒΟΦΪ¥σ÷Β, “≤ «Ήν¥σ÷Β, Φ¥≤ζΝΩΈΣ
±, Κ· ΐ»ΓΒΟΦΪ¥σ÷Β, “≤ «Ήν¥σ÷Β, Φ¥≤ζΝΩΈΣ![]() ΒΞΈΜ ±…ζ≤ζ’β≈ζ ‘ΦΝΒΡάϊ»σΉνΗΏ.
ΒΞΈΜ ±…ζ≤ζ’β≈ζ ‘ΦΝΒΡάϊ»σΉνΗΏ.

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΙέ≤λœ¬±μΘΚ
x | Θ≠3 | Θ≠2 | Θ≠1 | 1 | 2 | 3 |
fΘ®xΘ© | 5 | 1 | Θ≠1 | Θ≠3 | 3 | 5 |
gΘ®xΘ© | 1 | 4 | 2 | 3 | Θ≠2 | Θ≠4 |
‘ρf[gΘ®3Θ©Θ≠fΘ®Θ≠1Θ©]ΘΫ Θ® Θ©
A.3
B.4
C.Θ≠3
D.5
ΓΨΧβΡΩΓΩΫϋΡξά¥Έ“ΙζΒγΉ”…ΧΈώ––“Β”≠ά¥ΖΔ’ΙΒΡ–¬Μζ”ωΘ°2016ΡξΓΑ618Γ±ΤΎΦδΘ§Ρ≥ΙΚΈοΤΫΧ®ΒΡœζ έ“ΒΦ®ΗΏ¥ο516“Ύ‘Σ»ΥΟώ±“Θ°”κ¥ΥΆ§ ±Θ§œύΙΊΙήάμ≤ΩΟ≈ΆΤ≥ωΝΥ’κΕ‘Βγ…ΧΒΡ…ΧΤΖΚΆΖΰΈώΒΡΤάΦέΧεœΒΘ°œ÷¥”ΤάΦέœΒΆ≥÷–―Γ≥ω200¥Έ≥…ΙΠΫΜ“ΉΘ§≤ΔΕ‘ΤδΤάΦέΫχ––Ά≥ΦΤΘ§Ε‘…ΧΤΖΒΡΚΟΤά¬ ΈΣ0.6Θ§Ε‘ΖΰΈώΒΡΚΟΤά¬ ΈΣ0.75Θ§Τδ÷–Ε‘…ΧΤΖΚΆΖΰΈώΕΦΉω≥ωΚΟΤάΒΡΫΜ“ΉΈΣ80¥ΈΘ°
Θ®1Θ©―ΓΆξ≥…ΙΊ”Ύ…ΧΤΖΚΆΖΰΈώΤάΦέΒΡ![]() Ν–ΝΣ±μΘ§‘Ό≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.001ΒΡ«ΑΧαœ¬Θ§»œΈΣ…ΧΤΖΚΟΤά”κΖΰΈώΚΟΤά”–ΙΊΘΩ
Ν–ΝΣ±μΘ§‘Ό≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.001ΒΡ«ΑΧαœ¬Θ§»œΈΣ…ΧΤΖΚΟΤά”κΖΰΈώΚΟΤά”–ΙΊΘΩ
Θ®2Θ©»τΫΪΤΒ¬ ”ΈΣΗ≈¬ Θ§Ρ≥»Υ‘ΎΗΟΙΚΈοΤΫΧ®…œΫχ––ΒΡ3¥ΈΙΚΈο÷–Θ§…ηΕ‘…ΧΤΖΚΆΖΰΈώ»ΪΈΣΚΟΤάΒΡ¥Έ ΐΈΣΥφΜζ±δΝΩ![]() ΘΚ
ΘΚ
ΔΌ«σΕ‘…ΧΤΖΚΆΖΰΈώ»ΪΈΣΚΟΤάΒΡ¥Έ ΐ![]() ΒΡΖ÷≤ΦΝ–ΘΜ
ΒΡΖ÷≤ΦΝ–ΘΜ
ΔΎ«σ![]() ΒΡ ΐ―ßΤΎΆϊΚΆΖΫ≤νΘ°
ΒΡ ΐ―ßΤΎΆϊΚΆΖΫ≤νΘ°
ΗΫΝΌΫγ÷Β±μΘΚ
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ΒΡΙέ≤β÷ΒΘΚ
ΒΡΙέ≤β÷ΒΘΚ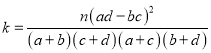 Θ®Τδ÷–
Θ®Τδ÷–![]() Θ©ΙΊ”Ύ…ΧΤΖΚΆΖΰΈώΤάΦέΒΡ
Θ©ΙΊ”Ύ…ΧΤΖΚΆΖΰΈώΤάΦέΒΡ![]() Ν–ΝΣ±μΘΚ
Ν–ΝΣ±μΘΚ
Ε‘ΖΰΈώΚΟΤά | Ε‘ΖΰΈώ≤Μ¬ζ“β | ΚœΦΤ | |
Ε‘…ΧΤΖΚΟΤά | 80 | ||
Ε‘…ΧΤΖ≤Μ¬ζ“β | 10 | ||
ΚœΦΤ | 200 |