题目内容
.(本小题满分12分)
设正数数列{an}的前n项和Sn满足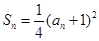 .
.
(1) 求a1的值;
(2) 证明:an=2n-1;
(3) 设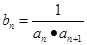 ,记数列{bn}的前n项为Tn,求Tn.
,记数列{bn}的前n项为Tn,求Tn.
设正数数列{an}的前n项和Sn满足
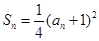 .
.(1) 求a1的值;
(2) 证明:an=2n-1;
(3) 设
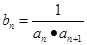 ,记数列{bn}的前n项为Tn,求Tn.
,记数列{bn}的前n项为Tn,求Tn.解:(1)由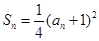 得
得 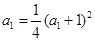 ,则a1=1. (2)∵
,则a1=1. (2)∵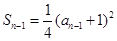
∴an=Sn-Sn-1=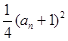 -
-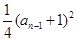 (n≥2),
(n≥2),
整理得 (an+an-1)(an-an-1-2)=0
∵an>0, ∴an+an-1>0
∴an-an-1-2=0,即an-an-1=2(n≥2).
∴{an}是等差数列,∴an=2n-1.
(3)∵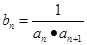 =
=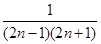 =
=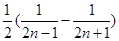
∴Tn=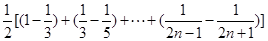 =
=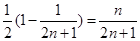 .
.
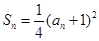 得
得 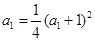 ,则a1=1. (2)∵
,则a1=1. (2)∵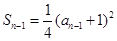
∴an=Sn-Sn-1=
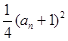 -
-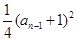 (n≥2),
(n≥2), 整理得 (an+an-1)(an-an-1-2)=0
∵an>0, ∴an+an-1>0
∴an-an-1-2=0,即an-an-1=2(n≥2).
∴{an}是等差数列,∴an=2n-1.
(3)∵
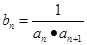 =
=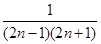 =
=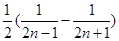
∴Tn=
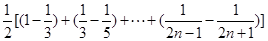 =
=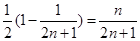 .
.略

练习册系列答案
相关题目
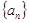 满足
满足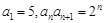 ,则
,则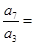 ( )
( )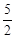
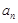 },
},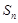 为其前n项的和,
为其前n项的和,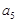 =6,
=6,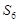 =18,n∈N*.
=18,n∈N*. I)求数列{
I)求数列{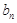 =3
=3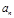 ,求数列{
,求数列{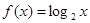 ,若
,若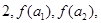
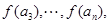
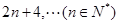 成等差数列.
成等差数列.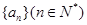 的通项公式;
的通项公式;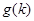 是不等式
是不等式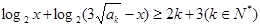 整数解的个数,求
整数解的个数,求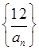 的前n项和为
的前n项和为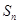 ,是否存在正数
,是否存在正数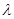 ,对任意正整数
,对任意正整数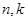 ,使
,使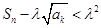 恒成立?若存在,求
恒成立?若存在,求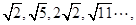 则
则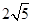 是这个数列的
是这个数列的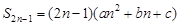 ,则
,则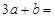 .
. 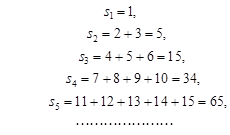
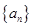 的前
的前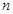 项和为
项和为 ,且
,且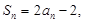 则
则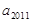 =
= 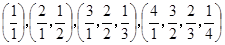 ,
,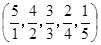 ,……
,……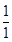 ,
,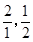 ,
,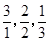 ,
,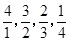 ,
,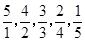
 ,……则此数列中的2012项是
,……则此数列中的2012项是