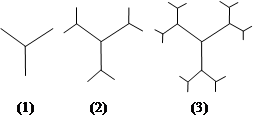题目内容
已知函数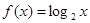 ,若
,若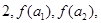
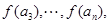
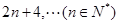 成等差数列.
成等差数列.
(1)求数列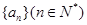 的通项公式;
的通项公式;
(2)设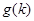 是不等式
是不等式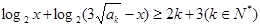 整数解的个数,求
整数解的个数,求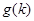 ;
;
(3)记数列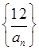 的前n项和为
的前n项和为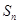 ,是否存在正数
,是否存在正数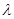 ,对任意正整数
,对任意正整数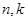 ,使
,使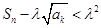 恒成立?若存在,求
恒成立?若存在,求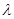 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
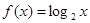 ,若
,若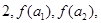
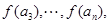
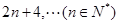 成等差数列.
成等差数列.(1)求数列
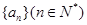 的通项公式;
的通项公式;(2)设
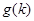 是不等式
是不等式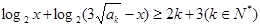 整数解的个数,求
整数解的个数,求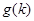 ;
;(3)记数列
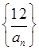 的前n项和为
的前n项和为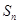 ,是否存在正数
,是否存在正数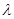 ,对任意正整数
,对任意正整数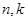 ,使
,使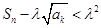 恒成立?若存在,求
恒成立?若存在,求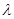 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.解:(1)由题可知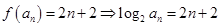 ………………(2分)
………………(2分)
得 .………………………………………………………………(4分)
.………………………………………………………………(4分)
(2)原式化简:
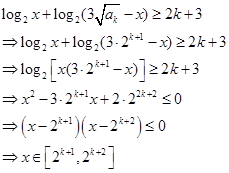 ……………………………………(8分)
……………………………………(8分)
其中整数个数 .…………………………………………(10分)
.…………………………………………(10分)
(3)由题意,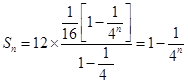 ,
,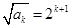 …………………(12分)
…………………(12分)
又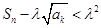 恒成立,
恒成立,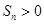 ,
,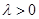 ,
,
所以当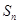 取最大值,
取最大值,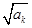 取最小值时,
取最小值时,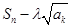 取到最大值.……(14分)
取到最大值.……(14分)
又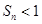 ,
,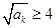 ,所以
,所以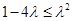 ……………………………………(16分)
……………………………………(16分)
解得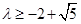 ………………………………………………………………(18分)
………………………………………………………………(18分)
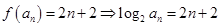 ………………(2分)
………………(2分)得
 .………………………………………………………………(4分)
.………………………………………………………………(4分)(2)原式化简:
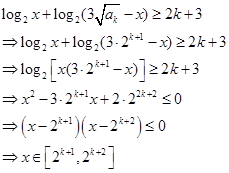 ……………………………………(8分)
……………………………………(8分)其中整数个数
 .…………………………………………(10分)
.…………………………………………(10分)(3)由题意,
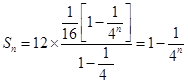 ,
,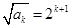 …………………(12分)
…………………(12分)又
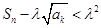 恒成立,
恒成立,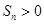 ,
,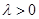 ,
,所以当
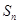 取最大值,
取最大值,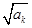 取最小值时,
取最小值时,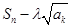 取到最大值.……(14分)
取到最大值.……(14分)又
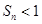 ,
,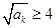 ,所以
,所以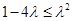 ……………………………………(16分)
……………………………………(16分)解得
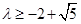 ………………………………………………………………(18分)
………………………………………………………………(18分)略

练习册系列答案
相关题目
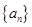 中,
中,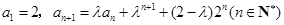 ,其中
,其中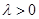 .
.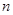 项和
项和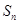 ;
;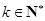 ,使得
,使得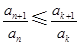 对任意
对任意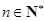 均成立.
均成立.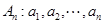 .如果数列
.如果数列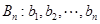 满足
满足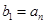 ,
,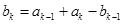 ,其中
,其中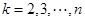 ,则称
,则称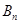 为
为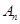 的“衍生数列”.
的“衍生数列”.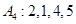 的“衍生数列”
的“衍生数列”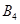 ;
;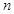 为偶数,且
为偶数,且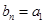 ;
;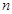 为奇数,且
为奇数,且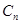 ,….依次将数
,….依次将数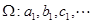 .证明:
.证明: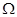 是等差数列.
是等差数列.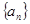 的前
的前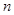 项和
项和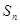 满足:
满足: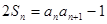 ,
,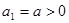
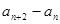 是一个定值;
是一个定值;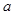 的取值范围;
的取值范围;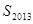 是一个整数,求符合条件的自然数
是一个整数,求符合条件的自然数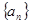 和
和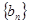 ,若对任意正整数
,若对任意正整数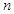 ,恒有
,恒有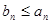 ,则称数列
,则称数列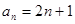 ,请写出一个公比不为1的等比数列
,请写出一个公比不为1的等比数列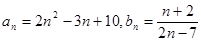 ,求证数列
,求证数列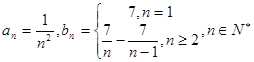 ,构造
,构造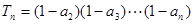 ,
,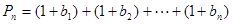 ,求使
,求使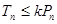 对
对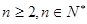 恒成立的
恒成立的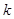 的最小值.
的最小值.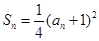 .
.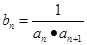 ,记数列{bn}的前n项为Tn,求Tn.
,记数列{bn}的前n项为Tn,求Tn.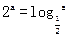 ,
,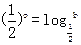 ,
,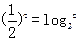 ,则a、b、c从小到大的顺序是_________________.
,则a、b、c从小到大的顺序是_________________.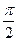 ),且cosa=a,sin(cosb)=b,cos(sinc)=c,则a、b、c从小到大的顺序是_____________
),且cosa=a,sin(cosb)=b,cos(sinc)=c,则a、b、c从小到大的顺序是_____________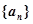 ,
,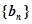 满足
满足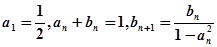
 ,则
,则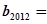 ▲ .
▲ . 其一半,图(3)用图(2)的方法在每一线段前端生成两条线段,长度为其一半,重复前面的作法至第n张图,设第n个图形所有线段长之和为an,第n个图形,最短的线段长之和为bn,设
其一半,图(3)用图(2)的方法在每一线段前端生成两条线段,长度为其一半,重复前面的作法至第n张图,设第n个图形所有线段长之和为an,第n个图形,最短的线段长之和为bn,设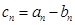 ,则cn=
,则cn=