题目内容
设点F1,F2分别为椭圆C:
+
=1的左、右焦点,点P为椭圆C上任意一点,则使得
•
=2成立的点P的个数为( )
| x2 |
| 9 |
| y2 |
| 5 |
| PF1 |
| PF2 |
| A.0 | B.1 | C.2 | D.4 |
设P(x0,y0),则
=(-2-x0,-y0),
=(2-x0,-y0),
由
•
=2,得(-2-x0,-y0)•(2-x0,-y0)=2,即x02+y02=6①,
又点P在椭圆上,所以
+
=1②,
联立①②解得
或
或
或
,
故满足题意的点P有4个,
故选D.
| PF1 |
| PF2 |
由
| PF1 |
| PF2 |
又点P在椭圆上,所以
| x02 |
| 9 |
| y02 |
| 5 |
联立①②解得
|
|
|
|
故满足题意的点P有4个,
故选D.

练习册系列答案
相关题目
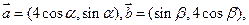
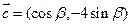 (1)若
(1)若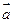 与
与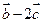 垂直,求
垂直,求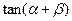 的值;(2)求
的值;(2)求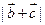 的最大值;
的最大值;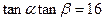 ,求证:
,求证: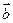 .
.