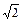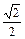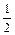题目内容
已知向量
=(sinθ，
)，
=(1，cosθ)，θ∈(-
，
)．
（1）若
⊥
，求θ；
（2）求|
+
|的最大值．
| a |
| 3 |
| b |
| π |
| 2 |
| π |
| 2 |
（1）若
| a |
| b |
（2）求|
| a |
| b |
（1）因为
⊥
，所以sinθ+
cosθ=0
得tanθ=-
又θ∈(-
，
)，
所以θ=-
（2）因为|
+
|2=(sinθ+1)2+(cosθ+
)2
=5+4sin(θ+
)
所以当θ=
时，|
+
|2的最大值为5+4=9
故|
+
|的最大值为3
| a |
| b |
| 3 |
得tanθ=-
| 3 |
又θ∈(-
| π |
| 2 |
| π |
| 2 |
所以θ=-
| π |
| 3 |
（2）因为|
| a |
| b |
| 3 |
=5+4sin(θ+
| π |
| 3 |
所以当θ=
| π |
| 6 |
| a |
| b |
故|
| a |
| b |
练习册系列答案
相关题目
，
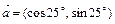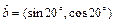，若t是实数，且
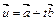，则
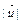的最小值为
