题目内容
如图,过点B(0,-b)作椭圆 =1(a>b>0)的弦,求这些弦长的最大值.
=1(a>b>0)的弦,求这些弦长的最大值.
 =1(a>b>0)的弦,求这些弦长的最大值.
=1(a>b>0)的弦,求这些弦长的最大值.
|BM|的最大值为2b.
设M(x,y)是椭圆上任一点.
|BM|2=x2+(y+b)2=x2+y2+2by+b2,由 =1,有x2=
=1,有x2= (b2-y2).
(b2-y2).
将其代入上式,整理,然后配方有
|BM|2=(1- )y2+2by+(a2+b2)
)y2+2by+(a2+b2)
=(1- )·(y-
)·(y- )2+
)2+ .
.
∵-b≤y≤b,
(1)当b≤c(即b≤ a)时,
a)时, ≤b,
≤b,
∴y= 时,|BM|的最大值为
时,|BM|的最大值为 ;
;
(2)当b>c(即b> a)时,
a)时, >b,故y=b时,点M在(0,b),即y轴上之顶点位置,|BM|2的最大值为(1-
>b,故y=b时,点M在(0,b),即y轴上之顶点位置,|BM|2的最大值为(1- )(b-
)(b- )2+
)2+ =4b2.
=4b2.
∴|BM|的最大值为2b.
|BM|2=x2+(y+b)2=x2+y2+2by+b2,由
 =1,有x2=
=1,有x2= (b2-y2).
(b2-y2).将其代入上式,整理,然后配方有
|BM|2=(1-
 )y2+2by+(a2+b2)
)y2+2by+(a2+b2)=(1-
 )·(y-
)·(y- )2+
)2+ .
.∵-b≤y≤b,
(1)当b≤c(即b≤
 a)时,
a)时, ≤b,
≤b,∴y=
 时,|BM|的最大值为
时,|BM|的最大值为 ;
;(2)当b>c(即b>
 a)时,
a)时, >b,故y=b时,点M在(0,b),即y轴上之顶点位置,|BM|2的最大值为(1-
>b,故y=b时,点M在(0,b),即y轴上之顶点位置,|BM|2的最大值为(1- )(b-
)(b- )2+
)2+ =4b2.
=4b2.∴|BM|的最大值为2b.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
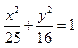 上一点,左、右焦点分别为F1,F2。
上一点,左、右焦点分别为F1,F2。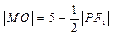
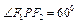 ,求
,求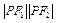 之值。
之值。 之间满足
之间满足
 ,求b的值
,求b的值 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值; ,如能,求解析式;如不能,再加什么条件就可使
,如能,求解析式;如不能,再加什么条件就可使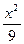 +
+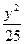 =1上到两个焦点距离之积最大的点的坐标是_______________.
=1上到两个焦点距离之积最大的点的坐标是_______________. =1(a>b>0)的左焦点F,A(-a,0)、B(0,b)是两个顶点.如果F到直线AB的距离等于
=1(a>b>0)的左焦点F,A(-a,0)、B(0,b)是两个顶点.如果F到直线AB的距离等于 ,那么椭圆的离心率为( )
,那么椭圆的离心率为( )



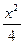 +y2=1相交于A、B两点,当t变化时,|AB|的最大值为( )
+y2=1相交于A、B两点,当t变化时,|AB|的最大值为( ) C.
C. D.
D.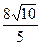




 -
- =1表示焦点在y轴上的椭圆,那么实数a的取值范围是…( )
=1表示焦点在y轴上的椭圆,那么实数a的取值范围是…( )