题目内容
【题目】已知直线l经过直线2x+y﹣5=0与x﹣2y=0的交点，且点A（5，0）到l的距离为3，则直线l的方程为 ．
【答案】4x﹣3y﹣5=0或x=2
【解析】解：联立 
，解得交点P（2，1）．
当直线l⊥x轴时，直线l的方程为：x=2，则点A（5，0）到l的距离为3，满足条件．
当直线l与x轴不垂直时，设直线l的方程为：y﹣1=k（x﹣2），∵点A（5，0）到l的距离为3，∴ 
=3，解得k= 
．
∴直线l的方程为：y﹣1= （x﹣2），化为：4x﹣3y﹣5=0．
综上可得：直线l的方程为：4x﹣3y﹣5=0或x=2．
所以答案是：4x﹣3y﹣5=0或x=2．
【考点精析】掌握点到直线的距离公式是解答本题的根本，需要知道点
到直线
的距离为：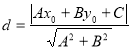
．
【题目】某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间(x个月)和市场占有率(y%)的几组相关对应数据：
x | 1 | 2 | 3 | 4 | 5 |
y | 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(1)根据上表中的数据，用最小二乘法求出y关于x的线性回归方程；
(2)根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过0.5%(精确到月)．
附： 
， 
.
【题目】某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图所示． 
（1）下表是年龄的频数分布表，求正整数a，b的值；
区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
人数 | 50 | 50 | a | 150 | b |
（2）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，年龄在第1，2，3组的人数分别是多少？
（3）在（2）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．
【题目】某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．
整理评分数据，将分数以
为组距分成
组：
，
，
，
，
，
，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
（Ⅰ）在抽样的100人中，求对A餐厅评分低于30的人数；
（Ⅱ）从对B餐厅评分在
范围内的人中随机选出2人，求2人中恰有1人评分在范围内的概率；
（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．
