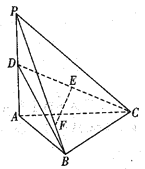
题目内容
【题目】已知F1,F2为椭圆C: ![]() 的左右焦点,点
的左右焦点,点![]() 为其上一点,且有
为其上一点,且有![]() .
.
(1)求椭圆C的标准方程;
(2)圆O是以F1,F2为直径的圆,直线l: y =k x + m与圆O相切,并与椭圆C交于不同的两点A,B,若![]() ,求k的值.
,求k的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析;(1)设椭圆![]() 的标准方程为
的标准方程为![]() ,由已知
,由已知![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的标准方程
的标准方程
(2)由直线![]() 与圆
与圆![]() 相切,得
相切,得![]() ,设
,设![]()
由 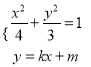 消去
消去![]() ,得
,得![]() ,利用韦达定理、根的判别式、向量的数量积,结合已知条件能求出
,利用韦达定理、根的判别式、向量的数量积,结合已知条件能求出![]() 的值..
的值..
试题解析;(1)由题意得: 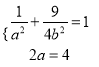 ,解得:
,解得: 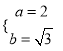 ,
,
则椭圆方程为![]() .
.
(2)由直线l与圆O相切,得 ![]() ,即m2=1+k2,
,即m2=1+k2,
设A(x1,y1)B(x2,y2),
由 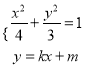 消去y,整理得:
消去y,整理得: ![]() ,
,
Δ=(8km)2-4(4m2-12)·(3+4k2)=16(9k2+6)>0恒成立,
所以 ![]() ,
,
![]()
∵m2=1+k2, ![]()
解得![]() .
.

练习册系列答案
相关题目