题目内容
【题目】在△ABC中,直线AB的方程为3x﹣2y﹣1=0,直线AC的方程为2x+3y﹣18=0.直线BC的方程为3x+4y﹣m=0(m≠25).
(1)求证:△ABC为直角三角形;
(2)当△ABC的BC边上的高为1时,求m的值.
【答案】
(1)证明:∵直线AB的斜率为 ![]() ,
,
直线AC的斜率为 ![]() ,kABkAC=﹣1,
,kABkAC=﹣1,
∴直线AB与AC互相垂直,因此,△ABC为直角三角形
(2)解:解方程组 ![]() ,得
,得 ![]() ,即A(3,4).
,即A(3,4).
设点A到直线BC的距离为d,则 ![]() .
.
由题意知d=1,即 ![]() ,即m=20或30
,即m=20或30
【解析】(1)利用斜率计算公式、直线垂直与斜率之间的关系即可判断出三角形形状.(2)利用直线的交点求法、点到直线的距离公式即可得出.
【考点精析】解答此题的关键在于理解点到直线的距离公式的相关知识,掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: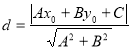 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某单位![]() 名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组
名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
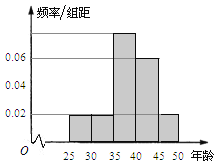
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(I)现要从年龄低于40岁的员工中用分层抽样的方法抽取12人,则年龄在第![]() 组的员工人数分别是多少?
组的员工人数分别是多少?
(II)为了交流读书心得,现从上述![]() 人中再随机抽取
人中再随机抽取![]() 人发言,设
人发言,设![]() 人中年龄在
人中年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(III)为了估计该单位员工的阅读倾向,现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查,调查结果如下表所示:(单位:人)
喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
男 | 14 | 4 | 18 |
女 | 8 | 14 | 22 |
合计 | 22 | 18 | 40 |
根据表中数据,我们能否有![]() 的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
附:![]() ,其中
,其中![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


