题目内容
【题目】如图,在平面直角坐标系中,点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),锐角α的终边与单位圆O交于点P.
,0),锐角α的终边与单位圆O交于点P. 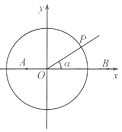
(Ⅰ)用α的三角函数表示点P的坐标;
(Ⅱ)当 ![]()
![]() =﹣
=﹣ ![]() 时,求α的值;
时,求α的值;
(Ⅲ)在x轴上是否存在定点M,使得| ![]() |=
|= ![]() |
| ![]() |恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
|恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
【答案】解:锐角α的终边与单位圆O交于点P.
(Ⅰ)用α的三角函数表示点P的坐标为(cosα,sinα);
(Ⅱ) ![]() ,
, ![]() ,
, ![]()
![]() =﹣
=﹣ ![]() 时,
时,
即(cos ![]() )(cos
)(cos ![]() )+sin2α=
)+sin2α= ![]() ,整理得到cos
,整理得到cos ![]() ,所以锐角α=60°;
,所以锐角α=60°;
(Ⅲ)在x轴上假设存在定点M,设M(x,0), ![]() ,
,
则由| ![]() |=
|= ![]() |
| ![]() |恒成立,得到
|恒成立,得到 ![]() =
= ![]() ,整理得2cosα(2+x)=x2﹣4,
,整理得2cosα(2+x)=x2﹣4,
所以存在x=﹣2时等式恒成立,所以存在M(﹣2,0).
【解析】(Ⅰ)用α的三角函数的坐标法定义得到P 坐标;(Ⅱ)首先写成两个向量的坐标根据 ![]()
![]() =﹣
=﹣ ![]() ,得到关于α的三角函数等式,求α的值;(Ⅲ)假设存在M(x,0),进行向量的模长运算,得到三角等式,求得成立的x值.
,得到关于α的三角函数等式,求α的值;(Ⅲ)假设存在M(x,0),进行向量的模长运算,得到三角等式,求得成立的x值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目