题目内容
【题目】已知函数f（x）=x2+ax+b（a，b∈R）． （Ⅰ）已知x∈[0，1]
（i）若a=b=1，求函数f（x）的值域；
（ii）若函数f（x）的值域为[0，1]，求a，b的值；
（Ⅱ）当|x|≥2时，恒有f（x）≥0，且f（x）在区间（2，3]上的最大值为1，求a2+b2的最大值和最小值．
【答案】解：（Ⅰ）（i），由已知，得f（x）=x2+x+1=（x+ 
）2+ 
，
又x∈[0，1]，
∴f（x）∈[1，3]，
∴函数f（x）的值域的值域为[1，3]，
（ii）函数y=f（x）的对称轴方程为x=﹣ 
①当﹣ ≤0时，即a≥0时，函数f（x）在[0，1]上单调性递增，可得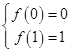 
，解得a=b=0，
②当﹣ ≥1时，即a≤﹣2时，函数f（x）在[0，1]上单调性递减，可得 
，解得a=﹣2，b=1，
③0＜﹣ ＜ 
时，即﹣1＜a＜0时，
，解得a=﹣4，b=4，或a=b=0（舍去），
④当 ≤﹣ ＜1，即﹣2＜a≤﹣1时， 
，解得a=±2，b=1，舍去，
综上所述a=b=0，或a=﹣2，b=1
（Ⅱ）由题意函数图象为开口向上的抛物线，且f（x）在区间（2，3]上的最大值只能在闭端点取得，
故有f（2）≤f（3）=1，从而a≥﹣5且b=﹣3a﹣8．
①若f（x）=0有实根，则△=a2﹣4b≥0，
在区间[﹣2，2]有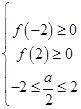 
即 
，将b=3a﹣8代入，整理得 
即a=﹣4，这时b=4，且△=0．
②若f（x）=0无实根，则△=a2﹣4b＜0，将b=﹣3a﹣8代入解得﹣8＜a＜﹣4．
综上﹣5≤a≤﹣4．
所以a2+b2=a2+（﹣3a﹣8）2=10a2+48a+64，在[﹣5，﹣4]单调递减，
故（a2+b2）min=32，（a2+b2）max=74．
【解析】（Ⅰ）（i）根据二次函数的性质即可求出函数的值域，（ii）根据二次函数的性质，分类讨论即可求出，（Ⅱ）因为若|x|≥2时，f（x）≥0，且f（x）在区间（2，3]上的最大值为1，f（x）在区间（2，3]上的最大值只能在闭端点取得，故有f（2）≤f（3）=1，从而a≥﹣5且b=﹣3a﹣8．在分类讨论基础上，将以上关系变为不等式组，消去c可得b的取值范围，最后将a2+b2转化为a的函数，求其值域可得a2+b2的最大值和最小值．
【考点精析】掌握二次函数在闭区间上的最值和二次函数的性质是解答本题的根本，需要知道当
时，当
时，
；当
时在
上递减，当时，
；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
