题目内容
【题目】如图,已知位于y轴左侧的圆C与y轴相切于点(0,1)且被x轴分成的两段圆弧长之比为1:2,过点H(0,t)的直线l于圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O. 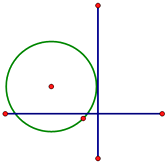
(1)求圆C的方程;
(2)当t=1时,求出直线l的方程;
(3)求直线OM的斜率k的取值范围.
【答案】
(1)解:因为位于y轴左侧的圆C与y轴相切于点(0,1),所以圆心C在直线y=1上,
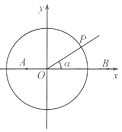
设圆C与x轴的交点分别为A、B,
由圆C被x轴分成的两段弧长之比为2:1,得 ![]() ,
,
所以CA=CB=2,圆心C的坐标为(﹣2,1),
所以圆C的方程为:(x+2)2+(y﹣1)2=4
(2)解:当t=1时,由题意知直线l的斜率存在,设直线l方程为y=mx+1,
由  得:
得: ![]() 或
或  ,
,
不妨令 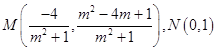 ,
,
因为以MN为直径的圆恰好经过O(0,0),
所以 ![]()
![]() =(
=( ![]() ,
, ![]() )(0,1)=
)(0,1)= ![]() =0,
=0,
解得 ![]() ,所以所求直线l方程为
,所以所求直线l方程为 ![]() 或
或 ![]()
(3)解:设直线MO的方程为y=kx,
由题意知, ![]() ,解之得
,解之得 ![]() ,
,
同理得, ![]() ,解之得
,解之得 ![]() 或k>0.由(2)知,k=0也满足题意.
或k>0.由(2)知,k=0也满足题意.
所以k的取值范围是 ![]() .
.
【解析】(1)由题意可知圆心在直线y=1上,设出圆与x轴的交点分别为A和B,由被x轴分成的两段圆弧长之比为1:2得到∠ACB的度数,根据直角三角形中30°角所对的直角边等于斜边的一半,得到半径AC和CB的长,进而得到圆心C的坐标,根据圆心坐标和圆的半径写出圆C的方程即可;(2)由t的值得到H的坐标,又直线l的斜率存在,设出直线l的方程,与圆的方程联立即可求出两交点坐标分别设为M和N,由以MN为直径的圆恰好经过坐标原点O,根据直径所对的圆周角为直角,得到 ![]() 与
与 ![]() 垂直,利用两向量垂直时数量积为0,列出关于m的方程,求出方程的解即可得到m的值,写出直线l的方程即可;(3)设出直线OM的方程,根据直线OM与圆的位置关系是相交,利用点到直线的距离公式表示出圆心到直线OM的距离d,让d小于圆C的半径列出关于k的不等式,求出不等式的解集即可得到k的取值范围.
垂直,利用两向量垂直时数量积为0,列出关于m的方程,求出方程的解即可得到m的值,写出直线l的方程即可;(3)设出直线OM的方程,根据直线OM与圆的位置关系是相交,利用点到直线的距离公式表示出圆心到直线OM的距离d,让d小于圆C的半径列出关于k的不等式,求出不等式的解集即可得到k的取值范围.
【考点精析】认真审题,首先需要了解圆的标准方程(圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程).
;圆心为A(a,b),半径为r的圆的方程).

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案