题目内容
【题目】已知对任意平面向量 ![]() =(x,y),把
=(x,y),把 ![]() 绕其起点沿逆时针方向旋转θ角得到的向量
绕其起点沿逆时针方向旋转θ角得到的向量 ![]() =(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
=(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
(1)已知平面内点A(2,3),点B(2+2 ![]() ,1).把点B绕点A逆时针方向旋转
,1).把点B绕点A逆时针方向旋转 ![]() 角得到点P,求点P的坐标.
角得到点P,求点P的坐标.
(2)设平面内曲线C上的每一点绕坐标原点沿顺时针方向旋转 ![]() 后得到的点的轨迹方程是曲线y=
后得到的点的轨迹方程是曲线y= ![]() ,求原来曲线C的方程.
,求原来曲线C的方程.
【答案】
(1)解:∵A(2,3), ![]() ,∴
,∴ ![]() ,
,
设点P的坐标为P(x,y),则 ![]()
![]() 绕点A逆时针方向旋转
绕点A逆时针方向旋转 ![]() 角得到:
角得到: ![]() =(4,0)
=(4,0)
∴(x﹣2,y﹣3)=(4,0)即 ![]() ,
,
∴ ![]() ,
,
即P(6,3)
(2)解:设旋转前曲线C上的点为(x,y),旋转后得到的曲线 ![]() 上的点为(x',y'),则
上的点为(x',y'),则 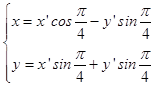 解得:
解得: 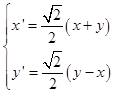
代入 ![]() 得x'y'=1即y2﹣x2=2
得x'y'=1即y2﹣x2=2
【解析】(1)求出 ![]() ,设点P的坐标为P(x,y),求出
,设点P的坐标为P(x,y),求出 ![]() ,
, ![]() 绕点A逆时针方向旋转
绕点A逆时针方向旋转 ![]() 角得到:
角得到: ![]() ,列出方程求解即可.(2)设旋转前曲线C上的点为(x,y),旋转后得到的曲线
,列出方程求解即可.(2)设旋转前曲线C上的点为(x,y),旋转后得到的曲线 ![]() 上的点为(x',y'),通过
上的点为(x',y'),通过 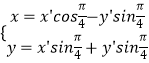 整合求解即可.
整合求解即可.
【考点精析】利用圆的一般方程对题目进行判断即可得到答案,需要熟知圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显.

练习册系列答案
相关题目