题目内容
【题目】已知函数f(x)=|ax﹣1|﹣(a﹣1)x
(1)当a= ![]() 时,满足不等式f(x)>1的x的取值范围为;
时,满足不等式f(x)>1的x的取值范围为;
(2)若函数f(x)的图象与x轴没有交点,则实数a的取值范围为 .
【答案】
(1)(2,+∞)
(2)[ ![]() ,1)
,1)
【解析】解:(1)a= ![]() 时,f(x)=|
时,f(x)=| ![]() x﹣1|+
x﹣1|+ ![]() x=
x= ![]() ,
,
∵f(x)>1,
∴ ![]() ,
,
解得x>2,
故x的取值范围为(2,+∞),(2)函数f(x)的图象与x轴没有交点,
①当a≥1时,f(x)=|ax﹣1|与g(x)=(a﹣1)x的图象:

两函数的图象恒有交点,
②当0<a<1时,f(x)=|ax﹣1|与g(x)=(a﹣1)x的图象:

要使两个图象无交点,斜率满足:a﹣1≥﹣a,
∴a≥ ![]() ,故
,故 ![]() ≤≤a<1
≤≤a<1
③当a≤0时,f(x)=|ax﹣1|与g(x)=(a﹣1)x的图象:
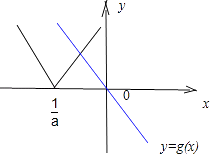
两函数的图象恒有交点,
综上①②③知: ![]() ≤a<1
≤a<1
故答案为:(2,+∞),[ ![]() ,1)
,1)
(1)化为分段函数,再解不等式即可,(2)①)当a≥1②当0<a<1③当a≤0三种情况,画出f(x)=|ax﹣1|与g(x)=(a﹣1)x的图象,利用图象确定有无交点.

练习册系列答案
相关题目