题目内容
(本小题满分12分)设直线 与直线
与直线 交于
交于 点.
点.
(1)当直线 过
过 点,且与直线
点,且与直线 垂直时,求直线
垂直时,求直线 的方程;
的方程;
(2)当直线 过
过 点,且坐标原点
点,且坐标原点 到直线
到直线 的距离为
的距离为 时,求直线
时,求直线 的方程.
的方程.
 与直线
与直线 交于
交于 点.
点.(1)当直线
 过
过 点,且与直线
点,且与直线 垂直时,求直线
垂直时,求直线 的方程;
的方程;(2)当直线
 过
过 点,且坐标原点
点,且坐标原点 到直线
到直线 的距离为
的距离为 时,求直线
时,求直线 的方程.
的方程.(1) 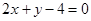 . (2)
. (2)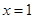 或
或 .
.
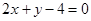 . (2)
. (2)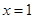 或
或 .
. 试题分析:由
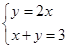 ,解得点
,解得点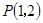 . ………………………2分
. ………………………2分(1)因为
 ⊥
⊥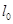 ,所以直线
,所以直线 的斜率
的斜率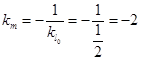 , ………………………4分
, ………………………4分又直线
 过点
过点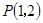 ,故直线
,故直线 的方程为:
的方程为: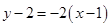 ,即
,即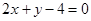 . …………………………6分
. …………………………6分(2)因为直线
 过点
过点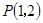 ,当直线
,当直线 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为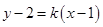 即
即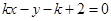 . …………………7分
. …………………7分所以坐标原点
 到直线
到直线 的距离
的距离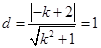 ,解得
,解得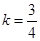 , …………9分
, …………9分因此直线
 的方程为:
的方程为: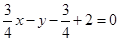 ,即
,即 . …………10分
. …………10分当直线
 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为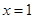 ,验证可知符合题意.
,验证可知符合题意.综上所述,所求直线
 的方程为
的方程为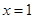 或
或 . ………………12分
. ………………12分点评:典型题,在直线与直线的位置关系问题中,平行、垂直是两类常见题型,如果利用斜率关系加以研究,必须考虑直线斜率不存在的可能情况。(2)是易错题。

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
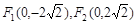 ,离心率
,离心率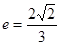 。
。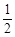 ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。 的一个焦点为
的一个焦点为 ,点
,点 在椭圆
在椭圆 上,点
上,点 满足
满足 (其中
(其中 为坐标原点), 过点
为坐标原点), 过点 作一斜率为
作一斜率为 的直线交椭圆于
的直线交椭圆于 、
、 两点(其中
两点(其中 轴上方,
轴上方,
 ,求
,求 的面积;
的面积; 为点
为点 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.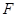 为左焦点,当
为左焦点,当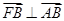 时,其离心率为
时,其离心率为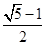 ,此类椭圆称为“黄金椭圆”,类比“黄金椭圆”,可推出“黄金双曲线”的离心率为 .
,此类椭圆称为“黄金椭圆”,类比“黄金椭圆”,可推出“黄金双曲线”的离心率为 . 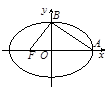
 分别为椭圆
分别为椭圆 的左、右焦点,点
的左、右焦点,点 为椭圆上任意一点,
为椭圆上任意一点,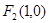 的距离的最大值为
的距离的最大值为 .
.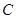 的方程。
的方程。 的坐标为
的坐标为 ,过点
,过点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆 两点。对于任意的
两点。对于任意的 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。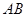 ,一个焦点为
,一个焦点为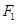 ,且
,且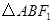 为等边三角形的椭圆的离心率是( )
为等边三角形的椭圆的离心率是( )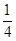
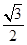
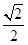
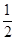
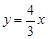 的双曲线的方程.
的双曲线的方程.