题目内容
(本题满分16分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分6分.
(文)已知椭圆 的一个焦点为
的一个焦点为 ,点
,点 在椭圆
在椭圆 上,点
上,点 满足
满足 (其中
(其中 为坐标原点), 过点
为坐标原点), 过点 作一斜率为
作一斜率为 的直线交椭圆于
的直线交椭圆于 、
、 两点(其中
两点(其中 点在
点在 轴上方,
轴上方, 点在
点在 轴下方) .
轴下方) .

(1)求椭圆 的方程;
的方程;
(2)若 ,求
,求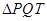 的面积;
的面积;
(3)设点 为点
为点 关于
关于 轴的对称点,判断
轴的对称点,判断 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.
(文)已知椭圆
 的一个焦点为
的一个焦点为 ,点
,点 在椭圆
在椭圆 上,点
上,点 满足
满足 (其中
(其中 为坐标原点), 过点
为坐标原点), 过点 作一斜率为
作一斜率为 的直线交椭圆于
的直线交椭圆于 、
、 两点(其中
两点(其中 点在
点在 轴上方,
轴上方, 点在
点在 轴下方) .
轴下方) .
(1)求椭圆
 的方程;
的方程;(2)若
 ,求
,求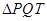 的面积;
的面积;(3)设点
 为点
为点 关于
关于 轴的对称点,判断
轴的对称点,判断 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.(1) (2)
(2)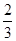 (3)
(3) 与
与 共线,设出点的坐标,用向量的坐标运算即可证明.
共线,设出点的坐标,用向量的坐标运算即可证明.
 (2)
(2)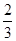 (3)
(3) 与
与 共线,设出点的坐标,用向量的坐标运算即可证明.
共线,设出点的坐标,用向量的坐标运算即可证明.试题分析:(1)由
 ,得 ……2分
,得 ……2分解得a2=2,b2=1,
所以,椭圆方程为
 . ……4分
. ……4分(2)设PQ:y=x-1,
由
 得3y2+2y-1=0, ……6分
得3y2+2y-1=0, ……6分解得: P(
 ),Q(0,-1),
),Q(0,-1),由条件可知点
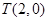 ,
,所以
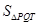 =
= |FT||y1-y2|=
|FT||y1-y2|=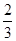 . ……10分
. ……10分(3) 判断:
 与
与 共线. ……11分
共线. ……11分设

则
 (x1,-y1),
(x1,-y1), =(x2-x1,y2+y1),
=(x2-x1,y2+y1), =(x2-2,y2), ……12分
=(x2-2,y2), ……12分由
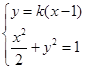 得
得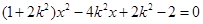 . ……13分
. ……13分(x2-x1)y2-(x2-2)(y1+y2)=(x2-x1)k(x2-1)-(x2-2)(kx1-k+kx2-k)
=3k(x1+x2)-2kx1x2-4k=3k
 -2k
-2k -4k
-4k=k(
 )=0. ……15分
)=0. ……15分所以,
 与
与 共线. ……16分
共线. ……16分点评:高考中圆锥曲线的题目一般难度较大,而且一般运算量较大,要仔细运算,更要结合图形数形结合简化求解过程.

练习册系列答案
相关题目
 ,右焦点
,右焦点 ,双曲线的实轴为
,双曲线的实轴为 ,
, 为双曲线上一点(不同于
为双曲线上一点(不同于 ),直线
),直线 ,
, 分别与直线
分别与直线 交于
交于 两点
两点 是否为定值,若为定值,求出该值;若不为定值,说明理由。
是否为定值,若为定值,求出该值;若不为定值,说明理由。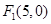 ,
,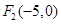 ,曲线上的点P到
,曲线上的点P到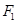 、
、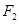 的距离之差的绝对值是6,则该曲线的方程为( )
的距离之差的绝对值是6,则该曲线的方程为( )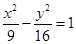
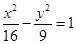
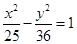
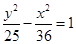
 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若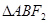 是钝角三角形,则该双曲线离心率的取值范围是
是钝角三角形,则该双曲线离心率的取值范围是

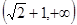

 的一个焦点为
的一个焦点为 ,点
,点 在椭圆
在椭圆 上,点
上,点 满足
满足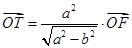 (其中
(其中 为坐标原点),过点
为坐标原点),过点 作一直线交椭圆于
作一直线交椭圆于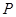 、
、 两点 .
两点 . 面积的最大值;
面积的最大值; 为点
为点 轴的对称点,判断
轴的对称点,判断 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.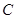 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上,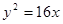 的准线交于
的准线交于 两点,
两点, ;则
;则 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )


 与直线
与直线 交于
交于 点.
点. 过
过 垂直时,求直线
垂直时,求直线 到直线
到直线 时,求直线
时,求直线 ,离心率为0.6,求椭圆的标准方程。
,离心率为0.6,求椭圆的标准方程。