题目内容
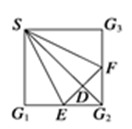
如图,四边形 中(图1),
中(图1),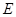 是
是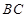 的中点,
的中点,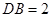 ,
,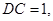
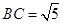 ,
,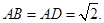 将(图1)沿直线
将(图1)沿直线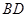 折起,使二面角
折起,使二面角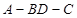 为
为 (如图2)
(如图2)
(1)求证: 平面
平面 ;
;
(2)求二面角A—DC—B的余弦值。
 中(图1),
中(图1), 是
是 的中点,
的中点,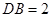 ,
,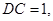
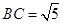 ,
,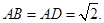 将(图1)沿直线
将(图1)沿直线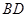 折起,使二面角
折起,使二面角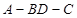 为
为 (如图2)
(如图2)(1)求证:
 平面
平面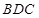 ;
;(2)求二面角A—DC—B的余弦值。

(1)见解析;
(2)
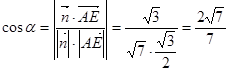
(2)
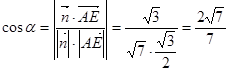
本题主要考察线面垂直的证明以及二面角的求法.一般在证明线面垂直时,先转化为证明线线垂直.进而得到线面垂直.
(1)先根据条件得到BD⊥平面AEM;进而通过求边长得到AE⊥ME;即可得到结论;
(2)先建立空间直角坐标系,求出两个半平面的法向量的坐标,再代入向量的夹角计算公式即可.
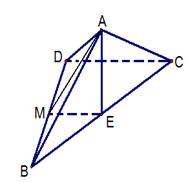
19.解:如图取BD中点M,连接AM,ME。∵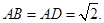
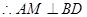
∵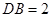 ,
,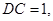
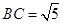
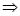
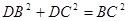 ,
,
所以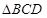 是BC为斜边的直角三角形,
是BC为斜边的直角三角形,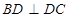 ,
,
∵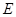 是
是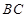 的中点,∴ME为
的中点,∴ME为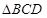 的中位线
的中位线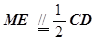 ,
,
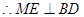 ,
,
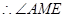 是二面角
是二面角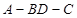 的平面角
的平面角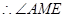 =
= …………………………3分
…………………………3分 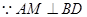 ,
,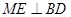 且AM、ME是平面AME内两相交于M的直线
且AM、ME是平面AME内两相交于M的直线
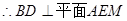
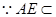 平面AEM
平面AEM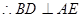
∵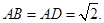 ,
,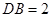
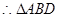 为等腰直角三角形
为等腰直角三角形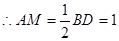 ,
,
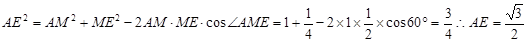
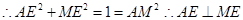
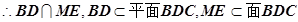
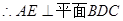 ………………6分
………………6分
(2)如图,以M为原点MB为x轴,ME为y轴,建立空间直角坐标系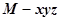 ,
,
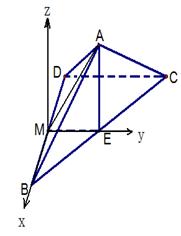
则由(1)及已知条件可知B(1,0,0),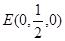 ,
,
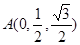 ,D
,D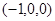 ,C
,C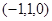 ,
,
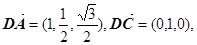
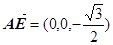 …………………8分
…………………8分
设平面ACD的法向量为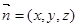
则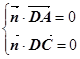
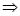
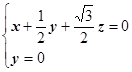
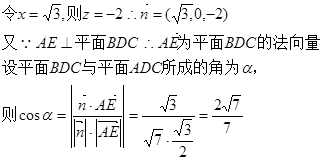
(1)先根据条件得到BD⊥平面AEM;进而通过求边长得到AE⊥ME;即可得到结论;
(2)先建立空间直角坐标系,求出两个半平面的法向量的坐标,再代入向量的夹角计算公式即可.

19.解:如图取BD中点M,连接AM,ME。∵
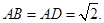
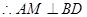
∵
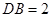 ,
,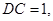
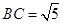
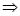
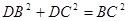 ,
, 所以
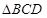 是BC为斜边的直角三角形,
是BC为斜边的直角三角形,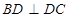 ,
, ∵
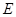 是
是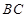 的中点,∴ME为
的中点,∴ME为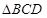 的中位线
的中位线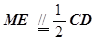 ,
, 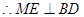 ,
,
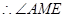 是二面角
是二面角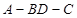 的平面角
的平面角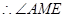 =
= …………………………3分
…………………………3分 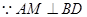 ,
,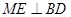 且AM、ME是平面AME内两相交于M的直线
且AM、ME是平面AME内两相交于M的直线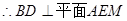
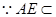 平面AEM
平面AEM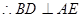
∵
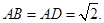 ,
,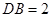
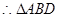 为等腰直角三角形
为等腰直角三角形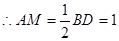 ,
,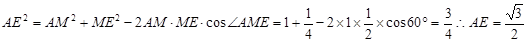
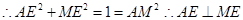
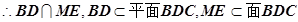
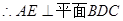 ………………6分
………………6分 (2)如图,以M为原点MB为x轴,ME为y轴,建立空间直角坐标系
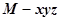 ,
, 
则由(1)及已知条件可知B(1,0,0),
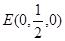 ,
,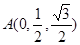 ,D
,D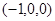 ,C
,C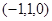 ,
,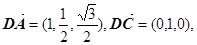
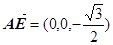 …………………8分
…………………8分 设平面ACD的法向量为
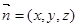
则
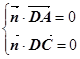
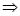
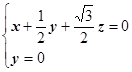

练习册系列答案
相关题目
 ,底面
,底面 是边长为
是边长为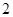 的正方形,
的正方形,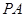 ⊥面
⊥面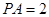 ,过点
,过点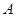 作
作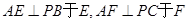 ,连接
,连接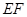 .
. ;
;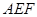 交侧棱
交侧棱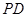 于点
于点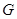 ,求多面体
,求多面体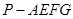 的体积.
的体积.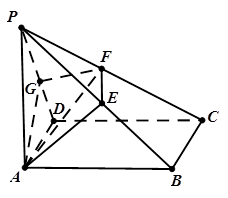
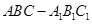 的侧棱与底面垂直,
的侧棱与底面垂直,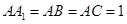 ,
,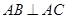 ,
,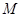 ,
,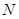 分别是
分别是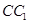 ,
,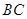 的中点,点
的中点,点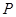 在直线
在直线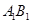 上,且
上,且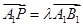 ;
;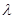 取何值,总有
取何值,总有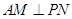 ;
;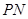 与平面
与平面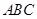 所成的角
所成的角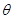 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;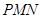 与平面
与平面
 ∩平面
∩平面 =AB,PQ⊥
=AB,PQ⊥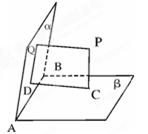
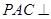 平面
平面 ,
,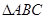 是以
是以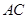 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,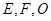 分别为
分别为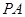 ,
,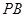 ,
,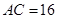 ,
,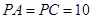 .
.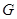 是
是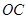 的中点,证明:
的中点,证明: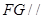 平面
平面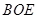 ;
; 内是否存在一点
内是否存在一点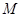 ,使
,使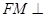 平面
平面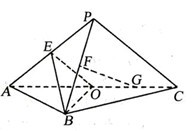
 G所在平面
G所在平面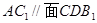 ;
;
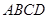 中,
中,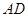 ⊥面
⊥面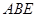 ,
,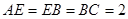 ,
,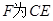 上的点,且
上的点,且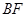 ⊥面
⊥面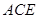 ,
,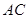 、
、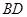 交于点
交于点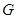 .
.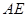 ⊥
⊥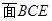 ;
;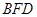 .
.
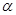 和直线l,则
和直线l,则