题目内容
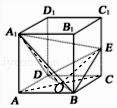
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,已知E为棱CC1上的动点. 
(1)求证:A1E⊥BD;
(2)是否存在这样的E点,使得平面A1BD⊥平面EBD?若存在,请找出这样的E点;若不存在,请说明理由.
【答案】
(1)证明:连接AC,设AC∩DB=O,连接A1O,OE.
∵A1A⊥底面ABCD,∴A1A⊥BD,又BD⊥AC,
∴BD⊥平面ACEA1,∵A1E平面ACEA1,
∴A1E⊥BD
(2)解:当E是CC1的中点时,平面A1BD⊥平面EBD.
证明如下:
∵A1B=A1D,EB=ED,O为BD中点,∴A1O⊥BD,EO⊥BD
∴∠A1OE为二面角A1﹣BD﹣E的平面角.
在正方体ABCD﹣A1B1C1D1中,设棱长为2a,
∵E为棱CC1的中点,由平面几何知识,EO= ![]() a,A1O=
a,A1O= ![]() a,A1E=3a,
a,A1E=3a,
∴A1E2=A1O2+EO2,即∠A1OE=90°.
∴平面A1BD⊥平面EBD
【解析】(1)连接AC,设AC∩DB=O,连接A1O,OE.证明A1A⊥BD,BD⊥AC,推出BD⊥平面ACEA1 , 然后证明A1E⊥BD.(2)当E是CC1的中点时,平面A1BD⊥平面EBD.说明∠A1OE为二面角A1﹣BD﹣E的平面角.设棱长为2a,推出∠A1OE=90°.即可证明平面A1BD⊥平面EBD.
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识,掌握垂直于同一个平面的两条直线平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
相关题目