Question

【题目】已知定义在[0，+∞）上的函数f（x）满足f（x）=3f（x+2），当x∈[0，2）时，f（x）=﹣x2+2x．设f（x）在[2n﹣2，2n）上的最大值为an（n∈N*） ， 且{an}的前n项和为Sn ， 则Sn的取值范围是（ ）
A.[1， ）
B.[1， ]
C.[ ，2）
D.[ ，2]

Answer 1

【答案】A
【解析】解：：∵函数f（x）满足f（x）=3f（x+2），

∴f（x+2）= f（x），即函数向右平移2个单位，最大值变为原来的 ，

又∵当x∈[0，2）时，f（x）=﹣x2+2x，∴a1=f（1）=1，∴数列{an}是首项为1、公比为 的等比数列，∴Sn= ∈ ．

所以答案是：A．

【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系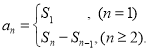才能正确解答此题．